Kezdőlap


Feladat:	F.3230	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Babos Attila , Baharev Ali , Bárány Kristóf , Bíró Anikó , Bujdosó Attila , Csikvári András , Devecsery András , Farkas Norbert , Gáspár Merse Előd , Gelencsér Gábor , Hangya Balázs , Harangi Viktor , Hartmann Miklós , Hegedűs Péter , Hermann György , Homolya Dániel , Horváth György , Juhász András , Keszegh Balázs , Kunszenti-Kovács Dávid , Kutalik Péter , Legány Csaba , Less Áron , Lippner Gábor , Lovas Róbert , Mansur Boase , Naszódi Gergely , Pál András , Páles Csaba , Pataki Péter , Poronyi Gábor , Puskás Péter , Sarlós Ferenc , Szabadka Zoltán , Szakács László , Székelyhidi Gábor , Szép László , Taraza Busra , Tisch Dávid , Vágvölgyi Péter , Végh A. László , Zábrádi Gergely
Füzet:	1998/november, 486 - 487. oldal		PDF \| MathML
Témakör(ök):	Pitagorasz-tétel alkalmazásai, Szögfelező egyenes, Vektorok skaláris szorzata, Síkgeometriai bizonyítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1998/április: F.3230

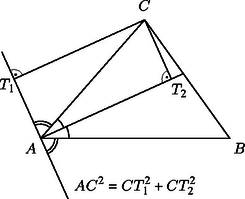
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismert, hogy egy háromszög ugyanazon csúcsához tartozó belső és külső szögfelező egyenesek merőlegesek egymásra (ábra). Ezért Pitagorasz tételéből következik, hogy egy háromszög egyik csúcsából egy másik csúcshoz tartozó külső és belső szögfelezőkre bocsátott merőleges szakaszok négyzetének összege megegyezik a két csúcsot összekötő oldal négyzetével. Vagyis a bizonyítandó állításunk

\begin{matrix} \begin{matrix} 6 (S A^{2} + S B^{2} + S C^{2}) = 2 (A B^{2} + B C^{2} + C A^{2}) \end{matrix} \end{matrix}

alakba írható.

Legyen

\vec{S A} = a

\vec{S B} = b

és

\vec{S C} = c

. Tudjuk, hogy ekkor

a + b + c = 0

. Ezért

{(a + b + c)}^{2} = 0

, azaz

\begin{matrix} a^{2} + b^{2} + c^{2} = - 2 (ab + bc + ca) . \end{matrix}

(1)

Másrészt viszont

\vec{A B} = \vec{A S} + \vec{S B} = b - a

, tehát

A B^{2} = b^{2} + a^{2} - 2 ab

; és hasonlóképpen

B C^{2} = c^{2} + b^{2} - 2 bc

C A^{2} = a^{2} + c^{2} - 2 ac

. Ezeket összeadva:

\begin{matrix} A B^{2} + B C^{2} + C A^{2} = 2 (a^{2} + b^{2} + c^{2}) - 2 (ab + bc + ca) . \end{matrix}

Vagyis (1)-et felhasználva:

\begin{matrix} A B^{2} + B C^{2} + C A^{2} = 3 (a^{2} + b^{2} + c^{2}) = 3 (S A^{2} + S B^{2} + S C^{2}) . \end{matrix}

Ezt 2-vel szorozva éppen a bizonyítandó állítást kapjuk.

Székelyhidi Gábor (Kuwait, New English School, 11. o.t.) dolgozata alapján