|
| Feladat: |
Gy.3186 |
Korcsoport: 14-15 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Andrássy Zoltán , Bárány Zsófi , Buruzs Ádám , Börcsök József , Csikvári Péter , Gelencsér Gábor , Gyenes Zoltán , Harangi Viktor , Horváth Dénes , Horváth György , Horváth Hedvig , Horváth Szilárd , Kiss Norbert , Lovrics Klára , Máthé András , Pozsár Balázs , Szászi Zsuzsanna , Szekeres Nóra , Varga Balázs , Wittner Lilla , Zábrádi Gergely |
| Füzet: |
1998/november,
484 - 485. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Magasságvonal, Súlyvonal, Háromszögek szerkesztése, Diszkusszió, Gyakorlat |
| Hivatkozás(ok): | Feladatok: 1998/február: Gy.3186 |
|
|
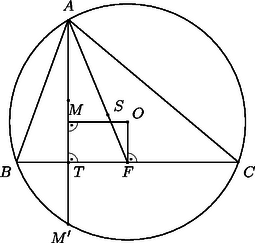
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Legyen az csúcsból húzott magasság, és súlyvonal, adott. Használjuk az ábra további jelöléseit is. Ismeretes, hogy bármely háromszög magasságpontjának egy oldalra vonatkozó tükörképe a körülírt körre illeszkedik. Az ábra (esetleg elfajuló) derékszögű háromszöge az feltétel mellett mindig megszerkeszthető. Mivel a körülírt kör egy húrja, ennek felező merőlegese és a egyenesre -ben állított merőleges a kör középpontjában metszik egymást. Az körüli sugarú kör a egyenesből kimetszi a , csúcsokat. A egyenes akkor is egyértelműen létezik, ha .
Diszkusszió: Már megállapítottuk, hogy szükséges. Ha , akkor két megoldás lehet, ugyanis elhelyezkedhet az szakaszon vagy annak -n túli meghosszabbításán. Ha az szakasz belső pontja, akkor az egyik megoldás hegyesszögű háromszög (ha , akkor derékszögű). A másik megoldás nyilván tompaszögű háromszög. Ha , akkor csak egy megoldás lesz, a tompaszögű. Megállapításaink az esetben is érvényesek, amikor is a megoldás(ok) egyenlő szárú háromszög(ek).
Hátravan még annak igazolása, hogy a és metszéspontok az feltétel esetén mindig létrejönnek. Az és háromszögek arányú hasonlósága révén (lásd még a II. megoldást). Ebből látható, hogy hegyesszögű és derékszögű háromszög megoldás esetén , tehát az körüli sugarú kör valóban metszi a egyenest. A tompaszögű megoldás esetén ez a metszés még nyilvánvalóbb, hiszen akkor és a más-más félsíkjában van. Végül belátjuk, hogy az esetben , és most is egy (derékszögű) megoldás van.
| Andrássy Zoltán (Fazekas M. Főv. Gyak. Gimn., 9. o.t.) |
II. megoldás. Tudjuk, hogy az , , pontok egy egyenesre illeszkednek (Euler-egyenes), és . Szerkesszük meg az háromszöget, majd ennek oldalán az pontot. Ezután a fenti arány alapján kapjuk az pontot. Az körüli sugarú kör és a egyenes közös pontjai a hiányzó csúcsok.
| Harangi Viktor (Fazekas M. Főv. Gyak. Gimn., 8. o.t.) |
|
|
 PDF |
PDF |  MathML
MathML