Kezdőlap


Feladat:	F.3218	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baharev Ali , Bíró Anikó , Biró Márton , Bíró Zsuzsanna , Bosznay Tamás , Bujdosó Attila , Devecsery Ágnes , Gazda Kinga , Gelencsér Gábor , Gueth Krisztián , Gyenes Zoltán , Hangya Balázs , Harangi Viktor , Hartmann Miklós , Hegedűs Péter , Hermann György , Homolya Dániel , Horváth Dénes , Horváth Gábor , Horváth György , Juhász András , Kunszenti-Kovács Dávid , Kurucz Ádám , Kutalik Péter , Legány Csaba , Léka Zoltán , Less Áron , Lippner Gábor , Lovas Róbert , Markó Péter , Mecz Balázs , Naszódi Gergely , Németh Ádám , Páles Csaba , Pap Júlia , Pataki Péter , Puskás Péter , Rácz Balázs , Sarlós Ferenc , Szabadka Zoltán , Szakács László , Terpai Tamás , Tisch Dávid , Tran Thanh Long , Végh A. László , Zawadowski Ádám , Zombori Tamás
Füzet:	1998/október, 416 - 418. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Háromszögek hasonlósága, Középponti és kerületi szögek, Feladat
Hivatkozás(ok):	Feladatok: 1998/február: F.3218

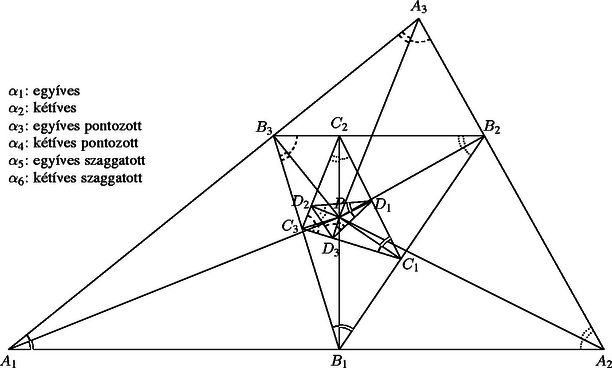
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $B_{i - 1} A_{i} P ∢ = α_{2 i - 1}$ és $P A_{i} B_{i} ∢ = α_{2 i}$ (l. az ábrát; az indexeket most is és a továbbiakban is modulo 3 értjük). A $P B_{i} A_{i} B_{i - 1}$ négyszög húrnégyszög, mert $P B_{i - 1} A_{i} ∢ = P B_{i} A_{i} ∢ = 90^{\circ}$ . Ezért a kerületi szögek tétele szerint:

\begin{matrix} P B_{i} B_{i - 1} ∢ = P A_{i} B_{i - 1} ∢ = α_{2 i - 1} és P B_{i - 1} B_{i} ∢ = P A_{i} B_{i} ∢ = α_{2 i} . \end{matrix}

(1)

(Az ábrán

B_{i}

A_{i} A_{i - 1}

szakasz belső pontja, könnyen látható azonban, hogy az (1) összefüggések akkor is igazak, ha

B_{i - 1}

és

B_{i}

közül az egyik nem belső pontja az

A_{i - 1} A_{i}

, illetve az

A_{i} A_{i + 1}

szakaszoknak.

B_{i - 1}

és

B_{i}

viszont egyszerre nem lehetnek az említett szakaszokon kívül, mert akkor

P

nem lenne belső pontja az

A_{1} A_{2} A_{3}

háromszögnek.) A

B_{1} B_{2} B_{3}

háromszög szögei az (1) összefüggések alapján tehát

\begin{matrix} \begin{matrix} B_{3} B_{1} B_{2} ∢ & = P B_{1} B_{3} ∢ + P B_{1} B_{2} ∢ = α_{1} + α_{4}, \\ B_{1} B_{2} B_{3} ∢ & = P B_{2} B_{1} ∢ + P B_{2} B_{3} ∢ = α_{3} + α_{6}, \\ B_{2} B_{3} B_{1} ∢ & = P B_{3} B_{2} ∢ + P B_{3} B_{1} ∢ = α_{5} + α_{2} . \end{matrix} \end{matrix}

Ezután a

B_{1} B_{2} B_{3}

háromszögből kiindulva ugyanúgy kapjuk a

C_{1} C_{2} C_{3}

háromszög szögeit:

\begin{matrix} C_{3} C_{1} C_{2} ∢ = α_{1} + α_{6}, C_{1} C_{2} C_{3} ∢ = α_{3} + α_{2} és C_{2} C_{3} C_{1} ∢ = α_{5} + α_{4}; \end{matrix}

majd pedig a

C_{1} C_{2} C_{3}

háromszögre alkalmazva az eljárást, a

D_{1} D_{2} D_{3}

háromszög szögeit:

\begin{matrix} D_{3} D_{1} D_{2} ∢ = α_{1} + α_{2}, D_{1} D_{2} D_{3} ∢ = α_{3} + α_{4} és D_{2} D_{3} D_{1} ∢ = α_{5} + α_{6} . \end{matrix}

Tehát a

D_{1} D_{2} D_{3}

háromszög szögei megegyeznek az

A_{1} A_{2} A_{3}

háromszög szögeivel, vagyis a két háromszög hasonló.

Megjegyzés. Az állítás megfelelője tetszőleges konvex

n

-szögre is igaz, akkor

n

lépés után kapunk az eredetihez hasonló

n

-szöget. A szögek egyenlőségét ebben az esetben is a megoldásban leírt módon láthatjuk be, a sokszögek hasonlósága azonban nem következik a szögek egyenlőségéből, ehhez még azt is meg kell mutatnunk, hogy

P

-nek a két sokszög megfelelő oldalegyeneseitől való távolságának aránya állandó.

Végh A. László (Debrecen, Fazekas M. Főv. Gyak. Gimn., 11. o.t.) dolgozata alapján