Kezdőlap


Feladat:	C.495	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ábrány Miklós , Antal István , Babos Attila , Bákor Krisztina , Birkner Tamás , Börcsök József , Csató György , Csizmadia Zsolt , Csornai Gyula , Farkas Melinda , Farkas Milán , Gajdos Béla , György László , Kalcsú Áron , Kiss Sándor , Kocsis Gábor , Kovács Adrián , Lengyel Zoltán , Lovas Róbert , Makó Veronika , Németh Ádám , Péterfalvi Ferenc , Pozsonyi Tamás , Sarlós Ferenc , Somlai Henrietta , Szigel Gábor , Szűcs Zsófia , Varga Zsolt , Zalán Péter , Závodi Attila
Füzet:	1998/október, 399. oldal		PDF \| MathML
Témakör(ök):	Trapézok, Geometriai egyenlőtlenségek, Külső szög tétel, C gyakorlat
Hivatkozás(ok):	Feladatok: 1998/február: C.495

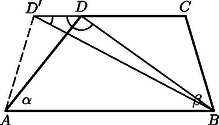
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alapon fekvő szögek $α$ és $β$ , és legyen $α < β$ ; ekkor azt állítjuk, hogy $A C > B D$ . Mérjük fel az $A$ csúcsban a $β$ szöget az ábra szerint. Ekkor az $A B C D'$ szimmetrikus trapézt kapjuk, amelyben $B D' = A C$ . A $D D' B$ háromszögből

\begin{matrix} D' D B ∢ > D C B ∢, \end{matrix}

(1)

hiszen

D' D B ∢

D C B

háromszög külső szöge, amiről tudjuk, hogy egyenlő a két nem szomszédos belső szög összegével.

\begin{matrix} D C B ∢ = D D' A ∢, \end{matrix}

(2)

mivel az

A B C D'

trapéz szimmetrikus. Másrészt

\begin{matrix} D D' A ∢ > D D' B ∢, \end{matrix}

(3)

az utóbbi szög ugyanis része az előzőnek. (1), (2) és (3)-ból

\begin{matrix} D' D B ∢ > D C B ∢ = D D' A ∢ > D D' B ∢ . \end{matrix}

Azaz a

D' D B

háromszögben

D' D B ∢ > D D' B ∢

, nagyobb szöggel szemben nagyobb oldal fekszik, ezért

A C = B D' > B D

. Ezt akartuk bizonyítani.