Feladat:	C.491	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Babos Attila ,  Boros M. Mátyás ,  Csóka Endre ,  Farkas Milán ,  Lovas Róbert
Füzet:	1998/október, 397. oldal		PDF  |  MathML
Témakör(ök):	Magasságvonal, Geometriai egyenlőtlenségek, C gyakorlat
Hivatkozás(ok):	Feladatok: 1998/január: C.491

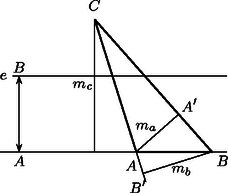
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Rajzoljunk egy $ABC$ háromszöget. Tegyük fel, hogy az $AB$ oldal kisebb, mint a hozzá tartozó magasság. Húzzuk meg az $AB$ egyenestől $AB$ távolságra haladó, $AB$-vel párhuzamos $e$ egyenest $AB$ azon felén, amelyiken a $C$ csúcs van. A $C$ csúcs messzebb van $AB$-től, mint az $e$ egyenes, a feltétel szerint ugyanis $AB<m_c$; ezért $CA>AB$ és $CB>AB$. Tehát $AB$ a háromszög (szigorúan) legkisebb oldala, ilyen oldal a háromszögben nincs több.  Lovas Róbert (Csongrád, Batsányi J. Gimn., 11. 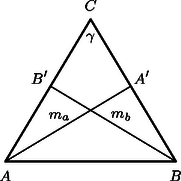o.t.) megoldása alapján   II. megoldás. Tegyük fel, hogy az $ABC$ háromszögben $\begin{array}{c}{\displaystyle a<m_a\text{és}b<m_b\mathrm{.}}\end{array}$ (1) Az $AA\text{'}C$ derékszögű háromszögből: $m_a=b\text{sin}\gamma$, a $BB\text{'}C$ háromszögből: $m_b=a\text{sin}\gamma$. Helyettesítsük be ezeket (1)-be, és adjuk össze az egyenlőtlenségek megfelelő oldalait; azt kapjuk, hogy $a+b<\left(a+b\right)\text{sin}\gamma$; $a+b\ne 0$-val egyszerűsítve a $\text{sin}\gamma >1$ összefüggést kapjuk, ami ellentmondás. Feltevésünk tehát nem lehet igaz.  Farkas Milán (Budapest, Városmajori Gimn., 11. o.t.)