Kezdőlap


Feladat:	F.3189	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Mizda Roland
Füzet:	1998/március, 162 - 163. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Szinusztétel alkalmazása, Beírt kör, Feladat
Hivatkozás(ok):	Feladatok: 1997/szeptember: F.3189

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szinusztételt alkalmazva a bizonyítandó állítás:

\begin{matrix} | \frac{a}{b} + \frac{b}{c} + \frac{c}{a} - \frac{b}{a} - \frac{c}{b} - \frac{a}{c} | < 1, \end{matrix}

azaz

\begin{matrix} - 1 < \frac{c - b}{a} + \frac{a - c}{b} + \frac{b - a}{c} < 1. \end{matrix}

(1)

Adjunk mindkét oldalhoz 3-at mindegyik egyenlőtlenségben:

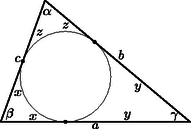
\begin{matrix} 2 < \frac{a + c - b}{a} + \frac{a + b - c}{b} + \frac{b + c - a}{c} < 4. \end{matrix}

Vezessük be az

a + b + c = 2 s

jelölést. 2-vel osztva:

\begin{matrix} 1 < \frac{s - b}{a} + \frac{s - c}{b} + \frac{s - a}{c} < 2. \end{matrix}

Jelöljük a háromszög beírt köréhez húzható érintő szakaszokat az ábra szerint. Ekkor

x + y + z = s

a = x + y

b = y + z

és

c = z + x

. A bizonyítandó egyenlőtlenség így alakul:

\begin{matrix} 1 < \frac{x}{x + y} + \frac{y}{y + z} + \frac{z}{z + x} < 2. \end{matrix}

(2)

A törtek eltávolítása és némi számolás után

(2)

mindkét egyenlőtlensége nyilvánvalóan teljesül. Mivel átalakításaink megfordíthatók, a feladat állítását igazoltuk.

Mizda Roland (Szombathely, Kanizsai Dorottya Gimn. 12. o. t.)

Megjegyzés. Már az

(1)

egyenlőtlenségek helyessége is közvetlenül megmutatható. Tegyük fel, hogy

\begin{matrix} a \leq b \leq c . \end{matrix}

(3)

A háromszög-egyenlőtlenség szerint

| c - b | < a

| a - c | < b

és

| b - a | < c

, tehát az

(1)

-ben szereplő törtek 1-nél kisebb abszolútértékűek.

(3)

miatt

\frac{a - c}{b}

negatív, de legalább akkora abszolútértékű, mint a pozitív

\frac{b - a}{c}

, ezért összegüknek

\frac{c - b}{a}

-val vett összege teljesíti

(1)

-et.
A teljesség érdekében végig kell vizsgálni az

a

b

c

nagyság szerinti felírásának

(3)

-hoz hasonló minden változatát.