Feladat:	3270. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ambrus Gergely ,  Szilágyi Tamás
Füzet:	2000/március, 179 - 181. oldal		PDF  |  MathML
Témakör(ök):	Mesterséges holdak, Newton-féle gravitációs erő, Impulzusváltozás törvénye (Impulzus), Gravitációs helyzeti energia, Feladat
Hivatkozás(ok):	Feladatok: 1999/szeptember: 3270. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A körpályán való keringés dinamikai feltétele: $\begin{array}{c}{\displaystyle m{a}_{\text{cp}}=m\frac{v_0^2}{2R}=\frac{fmM}{{\left(2R\right)}^2}\mathrm{,}{v}_0=\sqrt[]{\frac{fM}{2R}}\mathrm{.}}\end{array}$ Mivel a lendületváltozás iránya merőleges az eredeti lendületre, Pitagorasz tétele szerint $\begin{array}{c}{\displaystyle m{v}_1=\sqrt[]{{\left(m{v}_0\right)}^2+\Delta I^2}=\sqrt[]{2{\left(m{v}_0\right)}^2}\mathrm{,}}\end{array}$ ahonnan a műhold tömegével egyszerűsítve $\begin{array}{c}{\displaystyle v_1=\sqrt[]{2}{v}_0=\sqrt[]{\frac{fM}{R}}=7925\text{m/s}}\end{array}$ adódik. A műhold mechanikai energiája a lendületváltozás után $\begin{array}{c}{\displaystyle E=\frac{1}{2}m{v}_1^2-\frac{fmM}{2R}=\mathrm{0,}}\end{array}$ vagyis $v_1$ éppen a szökési sebesség. Eszerint a műhold a továbbiakban parabolapályán mozog. A műhold sebessége a Földhöz legközelebbi pontban a legnagyobb. Ekkor az energia- és a perdületmegmaradás miatt $\begin{array}{c}{\displaystyle v_{\text{max}}=\sqrt[]{\frac{2fM}{r_{\text{min}}}}\mathrm{,}2R{v}_0=r_{\text{min}}{v}_{\text{max}}\mathrm{.}}\end{array}$ Összevetve a két egyenletet $\begin{array}{c}{\displaystyle r_{\text{min}}=\frac{4R^2}{2fM}\frac{fM}{2R}=R=6370\text{km}\mathrm{,}}\end{array}$ $\begin{array}{c}{\displaystyle v_{\text{max}}=\sqrt[]{\frac{2fM}{R}}=11208\text{m/s}\mathrm{.}}\end{array}$  Szilágyi Tamás (Debrecen, KLTE Gyak. Gimn., 11. 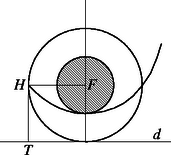o.t.) dolgozata alapján   II. megoldás. A parabolapálya Földhöz legközelebb eső pontját tisztán geometriai megfontolásokból is megkaphatjuk. A lendületváltozás utáni pillanatban a műhold sebessége (amely érintőirányú) ${45}^{\circ }$ szöget zár be a fókuszba húzott sugárral. A parabola ismert tulajdonságai miatt az érintő felezi a $THF$ szöget, így ez derékszög (lásd az ábrát). Mivel $HF$ párhuzamos a $d$ vezéregyenessel, $F$ és $H$ egyenlő ($2R$-nyi) távolságra vannak $d$-től, ami azt jelenti, hogy a parabola csúcspontja egyaránt $R$ távolságra lesz $F$-től és $d$-től.  Ambrus Gergely (Szeged, Radnóti M. Gimn., 11. o.t.) dolgozata alapján