Feladat:	3167. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bacsárdi László ,  Balogh Tímea ,  Kocsis Bence ,  Lengyel Tímea ,  Sarlós Ferenc ,  Szabó László
Füzet:	1999/február, 116 - 117. oldal		PDF  |  MathML
Témakör(ök):	Hullámterjedés 1 dimenzióban (kötélhullámok), Feladat
Hivatkozás(ok):	Feladatok: 1998/május: 3167. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Ha egy kezdetben nyugvó, hosszú kötél egyik végét $t$ ideig periodikusan mozgatjuk, akkor $P$ átlagos teljesítmény esetén $Pt$ munkát végzünk. Ezalatt a kötél $ct$ hosszúságú, tehát $m=\varrho ct$ tömegű darabja jön mozgásba. Számítsuk ki, mekkora átlagos mozgási és rugalmas energiája van ennek a kötéldarabnak! A kötél minden darabkája $A$ amplitúdójú, $\omega =2\pi f$ körfrekvenciájú harmonikus rezgőmozgást végez, tehát a legnagyobb sebessége $v_{\underset{}{\overset{}{\text{max}}}}=A\omega$. Ha a sebesség legnagyobb értékével számolnánk, akkor a mozgási energiára $\frac{1}{2}m{v}_{\underset{}{\overset{}{\text{max}}}}^2$ értéket kapnánk, de mivel a sebesség nagysága nulla és $v_{\underset{}{\overset{}{\text{max}}}}$ között váltakozik, az időben átlagolt mozgási energia (a váltóáramok effektív teljesítményéhez hasonlóan) a fenti értéknek csupán a fele: $\begin{array}{c}{\displaystyle E_{\text{mozg}}=\frac{1}{4}\varrho ct\cdot {\left(A\omega \right)}^2\mathrm{.}}\end{array}$ A kötélnek (ha benne hullámok terjednek) a helyzeti energiája is megnő. (Longitudinális hullámok esetén ez rugalmas energiát jelent, megfeszített kötélben terjedő transzverzális hullámoknál pedig a feszítőerőt létesítő súly gravitációs helyzeti energiájának növekedésével azonosítható.) A helyzeti energia átlagos értéke és a mozgási energia átlagos értéke ─ hasonlóan, mint egyetlen rezgő testnél ─ éppen egyenlő, a kötél teljes energiája tehát $E_{\text{teljes}}=2E_{\text{mozg.}}\mathrm{.}$ A munkatétel szerint $\begin{array}{c}{\displaystyle Pt=2\cdot \frac{1}{4}\varrho ct{A}^2{\omega }^2\mathrm{,}}\end{array}$ ahonnan a keresett átlagos teljesítmény $P=2c\varrho {\pi }^2{f}^2{A}^2$.   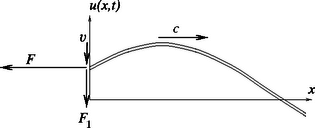II. megoldás. Egy $F$ erővel megfeszített kötélben $c=\sqrt[]{F/\varrho }$ sebességgel terjednek a transzverzális hullámok. Az $A$ amplitúdójú, $\omega$ körfrekvenciájú hullámokat leíró függvény: $\begin{array}{c}{\displaystyle u\left(x\mathrm{,}t\right)=A\text{sin}\omega \left(t-\frac{x}{c}\right)\mathrm{,}}\end{array}$ ahol $u\left(x\mathrm{,}t\right)$ a kötél végétől $x$ távolságra levő rész elmozdulása a $t$ időpillanatban. A kötél vége (az $x=0$ adattal jellemezhető pont) $\begin{array}{c}{\displaystyle v\left(t\right)=\frac{\Delta u\left(\mathrm{0,}t\right)}{\Delta t}=\frac{u\left(\mathrm{0,}t+\Delta t\right)-u\left(\mathrm{0,}t\right)}{\Delta t}=A\omega \text{cos}\omega t}\end{array}$ sebességgel mozog. (Kihasználtuk, hogy a szinuszfüggvény ,,változási üteme'' a koszinusz függvénnyel adható meg; ld. egy tömegpont harmonikus rezgőmozgását). Ugyanakkor a kötél végének ,,meredeksége'', vagyis térbeli változási üteme $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha =\frac{u\left(x+\Delta x\mathrm{,}t\right)-u\left(x\mathrm{,}t\right)}{\Delta x}=-\frac{A\omega }{c}\text{cos}\omega \left(t+\frac{x}{c}\right)\mathrm{.}}\end{array}$ A kötél meredeksége miatt a végpontjánál az $x$ tengely irányú $F$ nagyságú erő mellett egy arra merőleges $\begin{array}{c}{\displaystyle F_1\left(t\right)=-F\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \left(x=\mathrm{0,}t\right)=\frac{FA\omega }{c}\text{cos}\omega t}\end{array}$ erőt is ki kell fejtenünk. A pillanatnyi teljesítmény (amit a kötél végét mozgató ember fejt ki, illetve amelynek megfelelő ütemben csökken a kötél végén mozgó test energiája) $\begin{array}{c}{\displaystyle P\left(t\right)=F_1\left(t\right)\cdot v\left(t\right)=\frac{F{A}^2{\omega }^2}{c}\text{cos}{}^2\omega t\mathrm{.}}\end{array}$ Ennek a teljesítménynek időbeli átlaga (mivel $\text{cos}{}^2\omega t$ átlaga $\frac{1}{2}$) $\begin{array}{c}{\displaystyle P_{\text{átlag}}=\frac{1}{2c}F{A}^2{\omega }^2=\frac{1}{2}\varrho c{A}^2{\left(2\pi f\right)}^2\mathrm{.}}\end{array}$  Több dolgozat alapján