Kezdőlap


Feladat:	2487. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Patkó Eszter , Ujváry-Menyhárt Zoltán
Füzet:	1991/március, 136 - 137. oldal		PDF \| MathML
Témakör(ök):	Egyenletesen változó mozgás (Tömegpont mozgásegyenelete), Csúszó súrlódás, Nyomóerő, kötélerő, Geometriai szerkesztések alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1990/május: 2487. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Írjuk fel a testre ható erőket (1. ábra).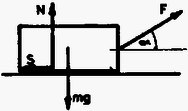

1. ábra

Függőleges irányban hat az

m g

súlyerő, az

N

nyomóerő és az

F

húzóerő függőleges komponense, vízszintes irányban az

S

súrlódási erő és a húzóerő vízszintes komponense. Függőleges irányban a test nem gyorsul, így:

\begin{matrix} N + F \cdot sin α = m g . \end{matrix}

Innen

\begin{matrix} N = m g - F sin α . \end{matrix}

Vízszintes irányban mozogjon

a

gyorsulással a test. Biztosan elindul, mert vízszintes húzóerőnél

\begin{matrix} S_{m a x} = μ N = μ m g = 6 N \end{matrix}

a tapadási súrlódás maximális értéke, a húzóerő pedig ekkor

10 N

.
A mozgásegyenlet vízszintes irányban:

\begin{matrix} m a = F cos α - S = F cos α - μ N = F cos α - μ m g + μ F sin α, \end{matrix}

innen

\begin{matrix} a = \frac{F}{m} (cos α + μ sin α) - μ g . \end{matrix}

A gyorsulás akkor maximális, ha a következő kifejezés maximális:

\begin{matrix} f (α) = cos α + μ sin α . \end{matrix}

(1)

Vezessük be a

μ = tgφ

összefüggéssel a

φ

határszöget. Ennek megfelelően

\begin{matrix} f (α) = cos α + tgφsinα=\frac{1}{cos φ}(cosαcosφ+sinαsinφ)=\frac{1}{cos φ}cos(α-φ). \end{matrix}

cos

függvény a

2 k π

helyeken maximális, ebből a számunkra értelmes megoldás:

\begin{matrix} α - φ = 0, \\ α = φ = arctg μ = 11, 31^{\circ} . \end{matrix}

Tehát a gyorsulás

α = 11, 31^{\circ}

mellett maximális.

II. megoldás. Vegyük fel a vektorábrát a 2. ábrán látható módon.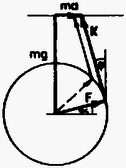

2. ábra

Először rajzoljuk be a súlyerőt, majd ennek végpontjába az adott nagyságú

F

húzóerőt, melynek végpontja egy kör mentén mozoghat. Ezután rajzoljuk be az asztal és a test közötti kölcsönhatási erőt,

K

-t. Ennek vízszintes komponense

μ N

nagyságú súrlódási erő, függőleges komponense az

N

nyomóerő.

K

-nak a függőlegessel bezárt

φ

szögére:

\begin{matrix} tgφ=μ. \end{matrix}

Az ábráról leolvasható, hogy

m a

akkor maximális, ha

K

éppen érinti a kört. Ekkor

α

és

φ

merőleges szárú szögek lesznek, tehát

α = φ = arctgμ=11,31^{\circ}

Patkó Eszter dolgozata alapján

III. megoldás. Az

(1)

egyenlet felírásáig ez a megoldás megegyezik az I.-vel. Ezután ábrázoljuk a koordinátarendszerben azokat a pontokat, amelyekre

x = cos α

és

y = μ sin α

. Ezek egy ellipszis pontjai, mivel

x^{2} + {(y / μ)}^{2} = 1

x + y

ott a legnagyobb, ahol az érintő az

x

tengellyel

135^{\circ}

-os szöget zár be, vagyis iránytangense

- 1

. Az ellipszist az

y

tengely mentén

1 / μ

arányban lapítva egy kört kapunk, melynek sugara egységnyi. A transzformáció után a keresett pontban az érintő iránytangense

- 1 / μ

, az érintési pontba húzott sugár iránytangense pedig

μ

lesz. Az érintési pontnak megfelelő

α

szögre:

\begin{matrix} μ = \frac{y'}{x'} = \frac{sin α}{cos α} = tg α, \\ α = arctg μ = 11, 31^{\circ} . \end{matrix}

Ujváry-Menyhárt Zoltán (Bp., Fazekas M. Gimn., II. o. t.)
dolgozata alapján