Kezdőlap


Feladat:	2443. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bak János , Dömötör Ákos , Horváth Ákos , Zóka Gábor
Füzet:	1990/november, 417 - 420. oldal		PDF \| MathML
Témakör(ök):	Bernoulli-törvény, Adiabatikus állapotváltozás, Analógia alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1989/december: 2443. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A tartály akkor kap impulzust, amikor a levegő molekulái a falaknak ütközve visszapattannak. Zárt tartály esetén az így kapott impulzusok eredője $0$ , nyitott tartálynál azonban a nyílásnál ,,elvész'' az impulzus, a tartály a kiáramló levegő által elvitt impulzussal azonos nagyságú, ellentétes irányú impulzust nyer, mint egy rakéta. Ha a hőközlés olyan gyors, hogy ezalatt a nyíláson nem áramlik ki levegő, akkor impulzust csak a hőközlés után kap a tartály. A hőközlés alatt munkavégzés nem történik, tehát

\begin{matrix} Q = Δ E = \frac{f}{2} N k Δ T és V Δ p = N k Δ T, \end{matrix}

amiből

\begin{matrix} Δ p = \frac{2 Q}{f \cdot V} = 4000 Pa, \end{matrix}

(a levegőre

f = 5

Δ p

lényegesen kisebb, mint a külső légnyomás, ezért a levegő áramlását a folyadékáramlásoknál megismert törvényekkel közelíthetjük (elhanyagolva ezzel a levegő sűrűségváltozását). A Bernoulli-egyenlet szerint

\begin{matrix} \frac{1}{2} ϱ v^{2} + ϱ g h + p = állandó . \end{matrix}

Esetünkben a

ϱ g h

‐ helyzeti energia jellegű ‐ tagot elhanyagolhatjuk, ezért a levegő kiömlési sebessége,

\begin{matrix} v = \sqrt[]{\frac{2 Δ p}{ϱ}} . \end{matrix}

Kiszámítjuk, mennyi az a ,,felesleges'' levegő, amelynek kiáramlása után a tartályban visszaáll a külső

p_{0}

nyomás. Az egyszerűség kedvéért tekintsük a levegő tágulását izoterm folyamatnak. A hőközlés után közvetlenül

\begin{matrix} (p_{0} + Δ p) V = \frac{m}{M} R T, \end{matrix}

(1)

a kiáramlás megszűnése után

\begin{matrix} p_{0} V = \frac{m - Δ m}{M} R T . \end{matrix}

A két egyenletből

\begin{matrix} Δ m = \frac{m}{p_{0} + Δ p} \cdot Δ p \approx m \frac{Δ p}{p_{0}}, \end{matrix}

kihasználtuk, hogy

\begin{matrix} Δ p ≪ p_{0} . \end{matrix}

Mivel a tartály fala hőszigetelő, ezért a levegő tágulása sokkal inkább tekinthető adiabatikus folyamatnak. Ekkor a kiáramlás megszűnte után

\begin{matrix} p_{0} V = \frac{m - Δ m}{M} R (T - Δ T) . \end{matrix}

(2)

Δ T

-t ki kell fejeznünk

Δ p

-vel. Adiabatikus folyamatokra

\begin{matrix} p V^{κ} = állandó és p^{(1 / κ) - 1} T = állandó . \end{matrix}

A második egyenlőségből

\begin{matrix} (\frac{1}{κ} - 1) p^{(1 / κ) - 2} Δ p T + p^{(1 / κ) - 1} Δ T = 0, \end{matrix}

azaz

\begin{matrix} Δ T = \frac{κ - 1}{κ} T \frac{Δ p}{p} . \end{matrix}

Δ T

-nek ezt a kifejezését a (2) egyenletbe helyettesítve, azt kivonva az (1) egyenletből és a másodrendűen kis tagokat elhagyva azt kapjuk, hogy

\begin{matrix} Δ m = \frac{m}{κ} \frac{Δ p}{p_{0}} . \end{matrix}

Az adiabatikus és izotermikus eredmény

1 / κ

szorzótényezőben különbözik egymástól. A levegőre

κ = \frac{7}{5}

, ezért számértékben a különbség nem nagy.
Sajnos

Δ p

‐ és ezzel

V

‐ időben változik (csökken), az időfüggést csak kissé haladottabb matematikai módszerek segítségével tudjuk meghatározni (lásd a II. megoldást). Azonban csak becslést kell adnunk, ezért számoljunk úgy, mintha az egész

Δ m

tömeg a kezdeti sebességgel áramlana ki a tartályból. Így az elvitt impulzus

\begin{matrix} Δ P = Δ m \cdot v = \frac{m}{κ} \frac{Δ p}{p_{0}} \sqrt[]{\frac{2 Δ p}{ϱ}} = \frac{4}{κ p_{0}} \sqrt[]{\frac{ϱ}{V}} {(\frac{\underline{O}}{f})}^{3 / 2} \approx 0, 06 \frac{kg m}{s} . \end{matrix}

II. megoldás. Az I. megoldásban eljutottunk addig, hogy ‐ a levegő sűrűségváltozását elhanyagolva ‐ a kiömlési sebesség

\begin{matrix} v = \sqrt[]{\frac{2 Δ p}{ϱ}}, \end{matrix}

(1)

és a nyomáskülönbség kezdeti értéke

\begin{matrix} Δ p = \frac{2 Q}{f \cdot V} . \end{matrix}

A levegő nyomása a tartályban két ok miatt csökken. Egyrészt azért, mert csökken a tartályban levő levegő mennyisége, másrészt azért, mert csökken a levegő hőmérséklete. Ha ez utóbbitól eltekintünk, azaz a folyamatot izotermikusnak tekintjük, akkor a nyomás időegység alatti csökkenése

\begin{matrix} \frac{d p}{d t} = \frac{d m}{d t} \frac{1}{V \cdot M} R T, \end{matrix}

(2)

ahol

\frac{d m}{d t}

az időegység alatt kiáramló levegő tömege,

M

a móltömeg A

d t

idő alatt kiáramló levegő egy

F

alapterületű,

v \cdot d t

hosszúságú hasábban helyezkedik el (l. ábra), ezért

\begin{matrix} d m = - ϱ F v d t, \end{matrix}

azaz

\begin{matrix} \frac{d m}{d t} = - ϱ F v, \end{matrix}

(3)

ahol

F

a nyílás keresztmetszete ‐ a negatív előjel arra utal, hogy a tartályban a levegő mennyisége csökken.

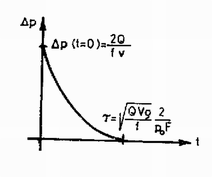A kiömlés kezdetekor

\begin{matrix} p V = \frac{m}{M} R T, \end{matrix}

(4)

az (1), (2), (3), (4) egyenletekből azt kapjuk, hogy

\begin{matrix} \frac{d p}{d t} = - \frac{p F}{V} \sqrt[]{\frac{2 Δ p}{ϱ}} . \end{matrix}

Δ p

nyomáskülönbségre érvényes egyenlet

\begin{matrix} \frac{d (Δ p)}{d t} = - \frac{p_{0} F}{V} \sqrt[]{\frac{2 Δ p}{ϱ}}, \end{matrix}

a gyök előtti

p

szorzótényezőben

Δ p

-t

p_{0}

mellett elhanyagoltuk.
Ezt a differenciálegyenletet könnyen megoldhatjuk, ha észrevesszük, hogy ugyanolyan szerkezetű, mint egy nehézségi erőtérben pattogó rugalmas labda mozgását leíró egyenlet (

Δ p

idő szerinti második differenciálhányadosa állandó). A

Δ p (t)

függvény képe parabola. Mivel

t = 0

esetén

\begin{matrix} Δ p = \frac{2 Q}{f \cdot V}, és \frac{d (Δ p)}{d t} = - \frac{2 p_{0} F}{V} \sqrt[]{\frac{Q}{f \cdot V \cdot ϱ}}, \end{matrix}

ezért

\begin{matrix} Δ p (t) = \frac{2 Q}{f \cdot V} - \frac{2 p_{0} F}{V} \sqrt[]{\frac{Q}{f \cdot V \cdot ϱ}} t + \frac{p_{0}^{2} F^{2}}{V^{2} ϱ} \frac{t^{2}}{2} = {(\sqrt[]{\frac{2 Q}{f \cdot V}} - \frac{p_{0} F}{V \sqrt[]{2 ϱ}} t)}^{2} \end{matrix}

A kiáramlás

\begin{matrix} τ = \sqrt[]{\frac{Q V ϱ}{f}} \frac{2}{p_{0} F} \end{matrix}

ideig tart (l. ábra). A kiáramló levegő

d t

idő alatt

\begin{matrix} d P = Δ p F \cdot d t \end{matrix}

impulzust visz el. Ezért az összes elvitt impulzus

\begin{matrix} Δ P = \int_{0}^{τ} Δ p F d t = F \int_{0}^{τ} Δ p d t . \end{matrix}

Az integrál éppen a parabola alatti területtel egyenlő, ami

\begin{matrix} \frac{1}{3} \cdot τ \cdot Δ p (t = 0) . \end{matrix}

Így

\begin{matrix} Δ P = \frac{4}{3 p_{0}} \sqrt[]{\frac{ϱ}{V}} {(\frac{Q}{f})}^{3 / 2} . \end{matrix}

Az I. megoldásban elmondottakhoz hasonlóan belátható, hogy adiabatikus tágulás esetén

\begin{matrix} Δ P = \frac{4}{3 p_{0} κ} \sqrt[]{\frac{ϱ}{V}} {(\frac{Q}{f})}^{3 / 2} . \end{matrix}