Kezdőlap


Feladat:	2120. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Czigány Zsolt , Horváth András , Kintli Lajos , Tasnádi Tamás , Tóth Tamás
Füzet:	1987/február, 92 - 94. oldal		PDF \| MathML
Témakör(ök):	Felületi feszültségből származó erő, Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1986/március: 2120. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A vízfelszínre helyezett alumíniumhuzalra a saját súlyán kívül hat a vízbe merült térfogattal arányos felhajtóerő, a felületi feszültségből és a $h$ besüllyedéssel arányos hidrosztatikai nyomásból származó erő; ezen erők egyensúlya alapján határozhatjuk meg a maximális huzalátmérőt. Mindegyik erő arányos a drót hosszával, így elegendő az egységnyi hosszra ható erőket kiszámítani.
Az egységnyi hosszúságú, $r$ sugarú Al huzal súlya $ϱ_{AI} \cdot g \cdot r^{2} π$ . A vízbe merült térfogatrész egy $2 ϑ$ központi szöggel jellemezhető körszelet, így a felfelé mutató felhajtóerő: $ϱ \cdot g r^{2} (ϑ - sin ϑ \cdot cos ϑ)$ , ahol $ϱ$ a víz sűrűsége.
A $h$ besüllyedésből adódó hidrosztatikai nyomás $ϱ \cdot g h$ , mely $2 r \cdot sin ϑ$ -val arányos keresztmetszetre $2 ϱ \cdot g h \cdot r sin ϑ$ nagyságú, a huzal súlyával ellentétes irányú erőt fejt ki.
A vízzel kétoldalt érintkező Al drótra a felületi feszültségből származó erő $2 α$ egységnyi hosszra vonatkoztatva. Az erők vektora az érintkezési vonalon a vízfelszín síkjában fekszik, így a vízszintes komponensek kétoldalt kiegyenlítik egymást, míg a függőleges komponensek eredője egy függőleges, felfelé mutató $2 α \cdot sin ϑ$ járulékot ad az előbbi erőkhöz.
A fentiek alapján felírható az egyensúly feltétele:

\begin{matrix} ϱ_{AI} g \cdot π r^{2} = ϱ \cdot g r^{2} (ϑ - sin ϑ \cdot cos ϑ) + 2 ϱ \cdot g h r sin ϑ + 2 α \cdot sin ϑ . \end{matrix}

(1)

A feladatban megadott

h

kifejezést (1)-be írva a keresett egyensúlyi sugárra az alábbi másodfokú egyenletet kapjuk:

\begin{matrix} (ϱ \cdot g (ϑ - sin ϑ \cdot cos ϑ) - π \cdot ϱ_{AI} g) r^{2} + \\ + (4 \sqrt[]{α \cdot ϱ \cdot g} sin \frac{ϑ}{2} sin ϑ) r + 2 α \cdot sin ϑ = 0. \end{matrix}

Osszuk el ezt az egyenletet

ϱ \cdot g

-vel és alkalmazzuk az

a = \sqrt[]{\frac{α}{ϱ \cdot g}}

jelölést, ekkor

\begin{matrix} (ϑ - sin ϑ \cdot cos ϑ - π \frac{ϱ_{AI}}{ϱ}) r^{2} + (4 sin ϑ / 2 \cdot sin ϑ) r \cdot a + 2 a^{2} sin ϑ = 0 \end{matrix}

adódik. Ebben az egyenletben adatként a dimenziótlan

ϱ_{AI} / ϱ = 2,7

mellett a hosszúság dimenziójú

a

szerepel, amelynek számértéke a függvénytáblázatban megtalálható adatokkal

\begin{matrix} a = \sqrt[]{\frac{0,0729 {N/m}^{2}}{9,81 {m/s}^{2} \cdot 1000 {kg/m}^{2}}} = 2,73 mm . \end{matrix}

Célszerű az

r

sugarat is ,,

a

-egységekben'' mérni, azaz

r = x \cdot a

a alakban keresni. Ezzel a dimenziótlan

x

mennyiségre a

\begin{matrix} (ϑ - sin ϑ \cdot cos ϑ - 2,7 π) x^{2} + (4 sin \frac{ϑ}{2} sin ϑ) x + 2 \cdot sin ϑ = 0 \end{matrix}

(2)

másodfokú egyenlet adódik.
Az egyenlet együtthatói a

ϑ

paramétertől függenek, amely

0

-tól

π

-ig változhat. A megoldóképlettel kifejezhetjük

r

-t a

ϑ

függvényében, és megkeresve a függvény maximumát, nyerjük a keresett maximális huzalátmérőt. Az itt vázolt módszer a differenciálszámítás elemeit felhasználva egy rendkívül bonyolult, csak numerikusan megoldható egyenletre vezet

ϑ

-ban. Ennél egyszerűbb, ha közvetlenül a (2) egyenletet használjuk a numerikus számoláshoz. Elegendően sűrűn (pl.

10^{\circ}

-onként) kiszámítjuk az adott

ϑ

szöghöz tartozó másodfokú egyenlet együtthatóit, majd ezekből az

x

gyököt. (A két gyök közül a pozitívat tartjuk meg.) Az

r

sugarat a

ϑ

függvényében ábrázolva kiválaszthatjuk a maximális

r

értéket. Szerencsére most már könnyen hozzájuthatunk kisebb személyi számítógépekhez, és így gyorsan és elegendő pontossággal végrehajthatjuk a numerikus számításokat. Egy lehetséges BASIC nyelvű programrészlet:

100 INPUT ,,SŰRŰSÉG''; RO
110 PRINT ,,KEZDŐ ÉS VÉGSZÖG''
120 INPUT ,,TK, TV:''; TK, TV
130 PRINT ,,A SZÖGTARTOMÁNY FELOSZTÁSÁNAK SZÁMA:''
140 INPUT ,,N:''; N
150 FOR I = 0 TO N
160 LET TT=TK+(TV‐TK)/N

*

I
170 LET TE=TT

*

PI/180
180 LET A=TE‐SIN(TE)

*

COS(TE)‐3, 14159

*

RO
190 LET B=4

*

SIN(TE/2)

*

SIN(TE):LET C=2

*

SIN(TE)
200 LET X=(‐B SQR(B

*

B‐4

*

*

C)/2/A
210 PRINT ,,SZÖG, SUGÁR=''; TT, X

*

2.73
220 NEXT I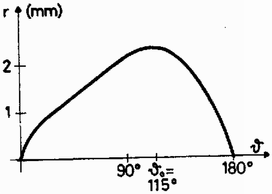

1. ábra

Az eredményt grafikonon ábrázoltuk (1. ábra). A bemenő adatok különböző értékei mellett egyre pontosabban adhatjuk meg a maximális

r

értéket. Két tizedesjegyre

ϑ_{0} = 115^{\circ}

-nál

r_{max} = 2,32

mm. A vízre helyezhető Al drót maximális átmérője

4,64

mm és ekkor

h = 4,59

mm a besüllyedés. A drót legalsó alkotója

h + r (1 + cos (180 - ϑ_{0})) = 7,89

mm mélyen van a víz felszíne alatt (2. ábra).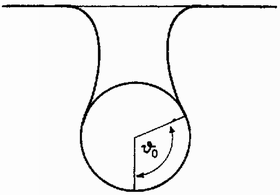

2. ábra

A megoldás fizikai jelentése és az egyensúlyi viszonyok stabilitása jól szemléltethető egy olyan ábrával, amelyen egy adott sugarú henger és a víz teljes energiáját tüntetjük fel a henger helyzetének (bemerülési mélységének) függvényében. Ezt a grafikont úgy kaphatnánk meg, ha a hengerre ható teljes erőt ‐ vagyis az (1) egyenlet jobb és bal oldalának különbségét ‐ megszoroznánk a henger kicsiny elmozdulásaival, s az így számított munkavégzéseket valamely önkényesen választott nullponttól kiindulva összegeznénk, integrálnánk. Az eredmény a 3. ábrán látható görbesereg lenne.

3. ábra

Amennyiben

r < r_{max}

, úgy két olyan

ϑ

érték is található, amelynél erőegyensúly valósul meg (lásd 1. ábra), vagyis ahol az energia-függvénynek szélső értéke van. A kisebb bemerülés stabil ‐, a nagyobb instabil egyensúlynak felel meg. A henger sugarát növelve

r = r_{max}

-nál a két egyensúlyi helyzet ,,összecsúszik'', az energiafüggvénynek pedig inflexiós pontja alakul ki. Ekkor és ennél nagyobb sugarú hengereknél semmilyen helyzetben nem lehet egyensúly, sőt már

r ≦ r_{max}

esetén is ‐ az energiafüggvény nagyon ,,sekély'' lokális minimuma miatt ‐ nagyon nehezen állítható be az egyensúlyi helyzet.

Megjegyzés. Kísérletileg is meghatározhatjuk az

r_{max}

értéket amely több körülmény befolyásoló hatása miatt eltérhet a fenti elméleti

r_{max}

értéktől. A felületi feszültség nem tiszta víz esetén megváltozik, a drót véges hosszúságú, és nagyon óvatosan kell a vízre tenni a zavarok elkerülése miatt. Tóth Tamás elvégezte a kísérletet, és szerinte

r > 1,5

mm esetén elsüllyed a drót.
A megoldás során hallgatólagosan feltételeztük, hogy a víz egyáltalán nem nedvesíti az alumíniumot, vagyis hogy a víz és a fém ún. illeszkedési szöge

\approx 180^{\circ}

. Ez szigorúan véve nem igaz, de a huzal felületének szennyeződése, ,,zsírossága'' miatt jó közelítésnek tekinthető.