Kezdőlap


Feladat:	1983. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Nyilas István László , Péter Oszkár
Füzet:	1985/november, 413. oldal		PDF \| MathML
Témakör(ök):	Tehetetlenségi nyomaték, Egyéb merev test síkmozgások, Rugalmas erő, Feladat
Hivatkozás(ok):	Feladatok: 1984/december: 1983. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $x_{1}$ és $x_{2}$ a bal, illetve a jobb oldali rugó megnyúlása az egyensúlyi helyzethez képest (1. ábra)! (A rugók egyensúlyi hosszába beleértjük a rúd súlya által okozott $M g / 2 k$ megnyúlást, ezért a súlyerőt a mozgásegyenletekben nem fogjuk figyelembe venni.)

1. ábra

A rúd tömegközéppontjának

a

gyorsulására és a tömegközéppont körüli

β

szöggyorsulásra felírt mozgásegyenletek:

\begin{matrix} M a = - k x_{1} - k x_{2}, \\ (1 / 12) M l^{2} β = (l / 2) x_{1} k - (l / 2) x_{2} k, \end{matrix}

ahol

M l^{2} / 12

a rúd tehetetlenségi nyomatéka. Az

x_{1}

és

x_{2}

elmozdulás kifejezhető a rugó tömegközéppontjának

x

elmozdulásával és a tömegközéppont körüli elfordulás

φ

szögével. Kis

φ

szögekre

\begin{matrix} x_{1} = x - (l / 2) φ; x_{2} = x + (l / 2) φ . \end{matrix}

Behelyettesítve a mozgásegyenletekbe:

\begin{matrix} a = - (2 k / M) x; β = - (6 k / M) φ . \end{matrix}

A két egyenletből leolvasható, hogy a rúd mozgása kétféle harmonikus rezgőmozgás összetétele:

ω = \sqrt[]{2 k / M}

frekvenciával rezeg a rúd tömegközéppontja függőleges irányban, és

\sqrt[]{3} ω

frekvenciával forgó rezgést végez a rúd tömegközéppontja körül.
A rúd két végének elmozdulása, figyelembe véve, hogy a kezdő pillanatban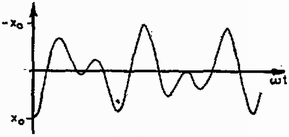

x_{1} = x_{0}

x_{2} = 0

{\dot{x}}_{1} = {\dot{x}}_{2} = 0;

\begin{matrix} x_{1,2} = x \pm \frac{φ l}{2} = \frac{x_{0}}{2} (cos ω t \pm cos \sqrt[]{3} ω t), \end{matrix}

azaz

\begin{matrix} x_{1} = x_{0} cos (\frac{\sqrt[]{3} - 1}{2} ω t) cos (\frac{\sqrt[]{3} + 1}{2} ω t), \\ x_{2} = x_{0} sin (\frac{\sqrt[]{3} - 1}{2} ω t) sin (\frac{\sqrt[]{3} + 1}{2} ω t), \end{matrix}

Megjegyzések. 1. A kitérések időfüggését ábrázolva (2. ábra) a csatolt rezgésekre jellemző lebegést figyelhetjük meg. Ez arra utal, hogy a rendszer felfogható harmonikus oszcillátorok csatolásaként is: a rúd jobb fele a jobb oldali rugóval, a bal fele pedig a bal oldali rugóval egy-egy oszcillátor. A csatolást köztük az okozza, hogy a rúd két felét mereven összeerősítették; a csatolás erős, ezért a lebegési frekvencia nem sokkal nagyobb az alapfrekvenciánál.

2. ábra

x

-et és

φ

-t a rendszer normálkoordinátáinak nevezzük. Bebizonyítható, hogy ha egy tetszőleges mechanikai rendszerre ható erők a stabil egyensúlyi helyzetből való kitéréseknek lineáris függvényei (a rugalmas erők ilyenek), akkor mindig található a független koordinátákkal megegyező számú normálkoordináta, amelyeket az jellemez, hogy egymástól függetlenül közönséges harmonikus rezgőmozgást végeznek.