Kezdőlap


Feladat:	1941. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Papp László , Steiber János
Füzet:	1984/december, 475 - 476. oldal		PDF \| MathML
Témakör(ök):	Lineáris hőtágulás, Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1984/május: 1941. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A melegítés során a négyzetből rombusz lett, ebből arra következtethetünk (l. a megjegyzést), hogy a két kitüntetett irány az átlók iránya (1. ábra).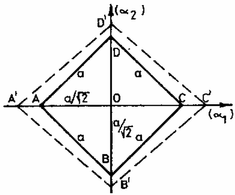

1. ábra

Így

A' C' = A C (1 + α_{1} t) = a \sqrt[]{2} (1 + α_{1} t)

és

B' D' = B D (1 + α_{2} t) = a \sqrt[]{2} (1 + α_{2} t)

.
A két egyenletet egymással elosztva a rombusz átlóinak arányát,

(1 + ε) - t

kapjuk:

\begin{matrix} 1 + ε = \frac{A' C'}{B' D'} = \frac{1 + α_{1} t}{1 + α_{2} t} . \end{matrix}

Innen

\begin{matrix} \frac{ε}{t} = \frac{α_{1} - α_{2}}{1 + α_{2} t} . \end{matrix}

Mivel

α_{2} t ≪ 1

, az előző egyenlőség helyett az alábbi közelítést vehetjük:

\begin{matrix} \frac{ε}{t} \approx α_{1} - α_{2} . \end{matrix}

(1)

A négyzet oldalának tágulására igaz, hogy az átlók által megszabott mértékben tágul. Így

\begin{matrix} A' B' = \sqrt[]{{(A O)}^{2} {(1 + α_{1} t)}^{2} + {(B O)}^{2} {(1 + α_{2} t)}^{2}} = \frac{a}{\sqrt[]{2}} \sqrt[]{{(1 + α_{1} t)}^{2} + {(1 + α_{2} t)}^{2}} . \end{matrix}

A négyzetre emelést elvégezve és a másodfokú tagokat elhanyagolva nyerjük, hogy

\begin{matrix} A' B' = a \sqrt[]{1 + (α_{1} + α_{2}) t} . \end{matrix}

Használjuk a

\sqrt[]{1 + x} \approx 1 + \frac{x}{2}

közelítést

(x ≪ 1)!

Így

\begin{matrix} A' B' = a (1 + \frac{α_{1} + α_{2}}{2} t) . \end{matrix}

A feladat szövege alapján

Δ = \frac{α_{1} + α_{2}}{2} t

, vagyis

\begin{matrix} \frac{2 Δ}{t} = α_{1} + α_{2} . \end{matrix}

(2)

(1) és (2) alapján

\begin{matrix} α_{1} = \frac{1}{2 t} (2 Δ + ε) és α_{2} = \frac{1}{2 t} (2 Δ - ε) . \end{matrix}

Megjegyzés. A megoldás első állításának (a két kitüntetett irány az átló) igazolására vegyünk fel egy koordináta-rendszert a kitüntetett irányokba mutató tengelyekkel (2. ábra)!

2. ábra

Vizsgáljuk meg, hogy az egyik tengellyel szöget bezáró szakasz hogyan tágul!
A megoldásban említettek szerint

\begin{matrix} l & = \sqrt[]{l_{0}^{2} cos^{2} β {(1 + α_{1} t)}^{2} + l_{0}^{2} sin^{2} β {(1 + α_{2} t)}^{2}} \approx l_{0} \sqrt[]{1 + 2 l (α_{1} cos^{2} β + α_{2} sin^{2} β)} \approx \\ \approx l_{0} [1 + (α_{1} cos^{2} β + α_{2} sin^{2} β) t] . \end{matrix}

Így az ,,eredő'' hőtágulási együttható

\begin{matrix} α = α_{1} cos^{2} β + α_{2} sin^{2} β = α_{1} + (α_{2} - α_{1}) sin^{2} β . \end{matrix}

Mivel esetünkben a négyzet oldalai egyenlően tágultak,

sin^{2} β

minden oldalra egyforma. Ez pedig azt jelenti, hogy a két kitüntetett irány megfelel az átlóknak.