Kezdőlap


Feladat:	1898. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Arany-Tóth László , Bíró Tamás , Horváth András , Kucsera Itala , Láng Róbert , Móré Gábor , Thaler Ferenc
Füzet:	1984/május, 231 - 233. oldal		PDF \| MathML
Témakör(ök):	Felületi feszültségből származó energia, Feladat
Hivatkozás(ok):	Feladatok: 1984/január: 1898. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A folyadékhártya a felületi feszültség miatt a minimális felszínű felületre igyekszik összehúzódni. Az összehúzódás mindig csak a kisebb felületű alak felé történhet, tehát a mozgás során a felület nem növekedhet.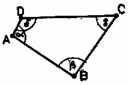

1. ábra

A keret alakját egyértelműen jellemzi az 1. ábrán jelölt

α

szög. Azt kell tehát megkeresnünk, milyen

α

szög esetén lesz a keret által meghatározott négyszög területe a legkisebb. Ehhez célszerű ábrázolni a négyszög területét,

F

-et, az

α

szög függvényében. Néhány esetben a négyszöget egyszerűen megszerkeszthetjük, ennek alapján az

α

szög könnyen megállapítható, ill. lemérhető,

F

pedig egyszerűen kiszámolható. Ezekben az esetekben a keret alakja a 2. ábrán látható;

α, (δ)

és

F

értékeit az alábbi táblázatban foglaltuk össze: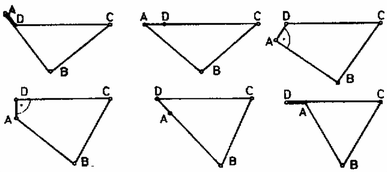

\begin{matrix} δ (^{\circ}) & 180 & 90 \\ α (^{\circ}) & 0 & 41 & 90 & 129 & 180 & 240 \\ F ({cm}^{2}) & 6 & 7, 94 & 10 & 10, 36 & 9, 17 & 6, 93 \end{matrix}

2. ábra

(Az ábráról azt is leolvashatjuk, hogy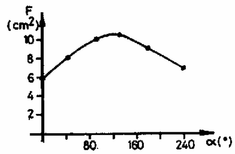

α

legfeljebb

240^{\circ}

lehet.) A 3. ábrán látható grafikonon ezeknek az eseteknek a bejelölt pontok felelnek meg. A grafikon további pontjait kaphatjuk meg, ha különböző

α

szögek esetén milliméter papíron megszerkesztjük az

A B C D

négyszöget, majd ,,leszámoljuk'' a területét. Így megkapjuk a 3. ábrán látható grafikont.

3. ábra

A grafikonról leolvashatjuk, hogy a négyszögnek van egy olyan állása, amikor területe a lehető legnagyobb. Ha

α

csökken vagy nő a maximális területhez tartozó

α_{0}

szöghöz képest, akkor a terület csökken. Ezért ha a keretet olyan helyzetben mártjuk az oldatba, amikor

α < α_{0}

, akkor

α = 0^{\circ}

-os helyzetűre húzza össze a felületi feszültség, ha pedig

α > α_{0}

, akkor

α = 240^{\circ}

-os helyzetűre.

Megjegyzés. A terület az 1. ábra jelöléseivel

\begin{matrix} F = \frac{1 \cdot 4 \cdot sin α}{2} + \frac{4 \cdot 5 \cdot sin γ}{2} . \end{matrix}

(1)

Írjuk fel a koszinusz-tételt az

A B D

és a

B C D

háromszögre:

\begin{matrix} B D^{2} = 1^{2} + 4^{2} - 2 \cdot 1 \cdot 4 \cdot cos α, \\ B D^{2} = 4^{2} + 5^{2} - 2 \cdot 4 \cdot 5 \cdot cos γ . \end{matrix}

E két egyenletből

\begin{matrix} cos γ = \frac{3 + cos α}{5} . \end{matrix}

Ezt az összefüggést és a

sin γ = \sqrt[]{1 - cos^{2} γ}

egyenlőséget felhasználva

\begin{matrix} F = 2 (sin α + \sqrt[]{25 - {(3 + cos α)}^{2}}) . \end{matrix}

Ez az

α

szög és a négyszög területe közötti pontos összefüggés.