Kezdőlap


Feladat:	1695. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Antal Tamás , Gulyás Gyula , Hatt János , Horváth Zoltán , Károlyi Gyula , Kiss János , Kovács Attila , Lakatos Róbert , Lóczi Géza , Mogyorósi András , Oszlányi Gábor , Pintér Gábor , Sáfár Péter , Szabó Endre , Tranta Beáta , Varga Kálmán
Füzet:	1981/november, 168 - 169. oldal		PDF \| MathML
Témakör(ök):	Tökéletesen rugalmas ütközések, Energiamegmaradás tétele, Impulzusmegmaradás törvénye, Szélsőérték differenciálszámítással, Feladat
Hivatkozás(ok):	Feladatok: 1981/február: 1695. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Két részecske rugalmas ütközését célszerű tömegközépponti rendszerben vizsgálni, mivel ebben a koordinátarendszerben a részecskék sebességének abszolút értéke változatlan marad, csak irányuk változik meg. Legyen az $M$ tömegű részecske ütközés előtti sebessége a laboratóriumban rögzített koordinátarendszerben $v_{0}$ . Ekkor a tömegközéppont sebessége $v_{T K} = v_{0} M / (M + m)$ . A tömegközépponti rendszerben az $M$ tömeg ütközés előtti sebessége $v_{0} - v_{T K}$ , ütközés utáni sebessége $| v_{0} - v_{T K} | \cdot e$ , ahol $e$ egy egységvektor, amelynek lehetséges irányait az impulzusmegmaradás határozza meg. Visszatranszformálva a laboratóriumi koordinátarendszerbe, az ütközés utáni sebesség:

\begin{matrix} v = v_{T K} + | v_{0} - v_{T K} | e = v_{0} \frac{M}{M + m} + v_{0} \frac{m}{M + m} e . \end{matrix}

(1)

Ábrázoljuk geometriailag az (1) egyenlettel adott vektor összeadást (1. ábra).

1. ábra

v

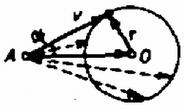vektor kezdőpontja

A

, végpontja egy

O

középpontú,

r = v_{0} m / (M + m)

sugarú gömbön van,

\bar{A O} = v_{0} M / (M + m)

. Mivel

M > m

A

a gömbön kívülre esik.

M

sebességének az iránya akkor változik a legtöbbet, ha

v

egyenese érinti a gömböt, ekkor

\begin{matrix} sin α = r / \bar{A O} = m / M . \end{matrix}

(2)

Beláthatjuk, hogy ez az eltérülési szög valóban megvalósítható

Sáfár Péter (Debrecen, Tóth Á. Gimn. III. o. t.)

II. megoldás. Tegyük fel, hogy az ütközés után

M

sebessége

α

m

sebessége

β

szöget zár be

M

v_{0}

kezdősebességével (2. ábra).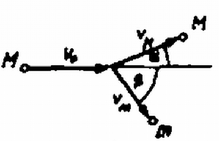

2. ábra

Felírhatjuk az impulzus és az energia megmaradását kifejező egyenleteket:

\begin{matrix} M v_{M} sin α = m v_{m} sin β & (3) \\ M v_{0} = M v_{M} cos α + m v_{m} cos β & (4) \\ (1 / 2) M v_{0}^{2} = (1 / 2) M v_{M}^{2} + (1 / 2) m v_{m}^{2} . & (5) \end{matrix}

Az egyenletrendszerből kifejezhetjük

α

-t

β

függvényében:

\begin{matrix} tg α = \frac{sin 2 β}{(M / m) - cos 2 β} . \end{matrix}

(6)

Deriválással megkaphatjuk azt a

β

szöget, amelynél

tg α

maximális, erre

cos 2 β = (m / M)

adódik. (6)-ba visszahelyettesítve a részecske maximális eltérülési szögére adódik:

\begin{matrix} tg α = \frac{m}{\sqrt[]{M^{2} - m^{2}}}, azaz sin α = m / M . \end{matrix}

(7)

Lakatos Róbert (Kalocsa, I. István Gimn. III. o. t.)