Feladat:	1093. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bari Ferenc ,  Korsós Gábor ,  Meszéna Géza ,  Németh József ,  Pályi Imre ,  Sparing László
Füzet:	1973/április, 187 - 189. oldal		PDF  |  MathML
Témakör(ök):	Egyéb gördülés (Gördülés), Feladat
Hivatkozás(ok):	Feladatok: 1972/december: 1093. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.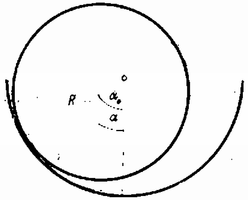   A henger, miközben súlypontja $\Delta h$-val mélyebbre, kerül, $v$ sebességre és $\omega$ szögsebességre tesz szert. Csúszásmentes gördülésnél alkalmazhatjuk a mechanikai energia megmaradásának törvényét: 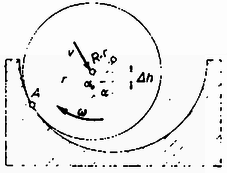$\begin{array}{c}{\displaystyle \left(1/2\right)m{v}^2+\left(1/2\right)\Theta {\omega }^2-mg\Delta h\mathrm{.}}\end{array}$ (1)   1. ábra   Az 1. ábráról leolvasható, hogy $\begin{array}{c}{\displaystyle \Delta h=\left(R-r\right)\left(\text{cos}\alpha -\text{cos}{\alpha }_0\right)\mathrm{,}}\end{array}$ (2) ezenkívül tudjuk, hogy egy homogén tömegeloszlású henger tehetetlenségi nyomatéka a szimmetriatengelyére vonatkoztatva $\Theta =m{r}^2/2$. Az (1) egyenletből csak akkor tudjuk meghatározni a sebességet, ha kiderítjük, hogy milyen megszorítást ad a csúszásmentes gördülés ténye $v$ és $\omega$ között. Írjuk fel a henger $A$ pontjának sebességét a vályúhoz képest! Ennek a pontnak a mozgása ‐ ugyanúgy, mint henger bármely más pontjáé ‐ két részből tehető össze. Egyrészt a súlypont haladó mozgásából adódóan $v$ sebességgel mozog az érintő irányában lefelé, másrészt a forgás miatt $r\omega$ sebessége van az érintő irányában felfelé. Az eredő $r\omega -v$ sebesség viszont a csúszásmentes gördülés miatt nulla kell, hogy legyen: $\begin{array}{c}{\displaystyle r\omega -v=0.}\end{array}$ (3) Az (1)-(3) egyenletrendszer megoldása: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle v=\sqrt[]{\left(4/3\right)g\left(R-r\right)\left(\text{cos}\alpha -\text{cos}{\alpha }_0\right)}\mathrm{,}}\hfill & \text{(<mn>4</mn>)}\\ \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \omega =\sqrt[]{\left(4/3\right)\left(g/r^2\right)\left(R-r\right)\left(\text{cos}\alpha -\text{cos}{\alpha }_0\right)}\mathrm{.}}\hfill & \text{(<mn>5</mn>)}\end{array}}$ A pályára kifejtett erő helyett kényelmesebb annak ellenerejét, vagyis a hengerre kifejtett erőt meghatároznunk. A hengerre a súlya és a vályú által kifejtett erő hat. Az utóbbit célszerű sugár irányú nyomóerőre és érintőleges súrlódási erőre bontani (2. ábra). 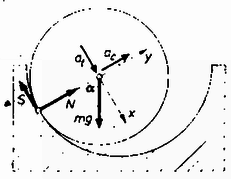  2. ábra   Ezen erők hatására a henger $\beta$ szöggyorsulással, súlypontja $a_c$ centripetális és $a_i$ érintőleges gyorsulással mozog. Írjuk fel a Newton egyenletet olyan koordináta-rendszerben, melynek $x$-tengelye érintőirányú, $y$-tengelye pedig sugárirányú! A forgómozgás alapegyenlete szerint $\begin{array}{c}{\displaystyle Sr=\Theta \beta \mathrm{.}}\end{array}$ (8) A csúszásmentes gördülés feltétele, (3) kis megváltozásokra is igaz: $\begin{array}{c}{\displaystyle \Delta v=r\Delta \omega \mathrm{.}}\end{array}$ A megváltozás $\Delta t$ időtartamával osztva látható, hogy $\begin{array}{c}{\displaystyle a_t=r\beta \mathrm{.}}\end{array}$ (9) A centripetális gyorsulásra az $a_c=v^2/\left(R-r\right)$ képletből (4) felhasználásával kapjuk: $\begin{array}{c}{\displaystyle a_c=\left(4/3\right)g\left(\text{cos}\alpha -\text{cos}{\alpha }_0\right)\mathrm{.}}\end{array}$ A (6)‐(9) egyenletek megoldása az erőkre