Kezdőlap


Feladat:	1052. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ábrahám Tibor , Mester Tamás , Meszéna Géza , Németh József , Prőhle Péter , Vladár Károly
Füzet:	1972/december, 230 - 233. oldal		PDF \| MathML
Témakör(ök):	Erők forgatónyomatéka, Tapadó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1972/április: 1052. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Célszerű először a geometriai viszonyokat tisztáznunk. Ha $n$ darab $r$ sugarú golyóból szorosan egy szabályos sokszöget rakunk ki, akkor az 1. ábra szerint a golyók középpontjának és a sokszög középpontjának távolsága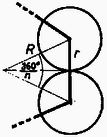

1. ábra

\begin{matrix} R = \frac{r}{sin 180^{\circ} / n} . \end{matrix}

(1)

A középre helyezett golyó csak akkor támaszkodik a többire, ha

\begin{matrix} R < 2 r, vagyis  ha n < 6. \end{matrix}

Ellenkező esetben valamennyi golyó az asztallapon nyugszik és nyilvánvalóan súrlódás nélkül is egyensúlyban van. Elegendő tehát az

n = 3

, 4 és 5 eseteket vizsgálnunk.
Válasszunk ki egy golyót az alsók közül és rajzoljuk le ezt, valamint a középső golyót oldalnézetből (2. ábra).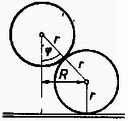

2. ábra

A későbbiekben szükségünk lesz a golyók középpontját összekötő egyenes és a függőleges által bezárt

φ

szög nagyságára. A 2. ábráról leolvasható, hogy

\begin{matrix} sin φ = \frac{R}{2 r}, \end{matrix}

vagyis (1) felhasználásával

\begin{matrix} sin φ = \frac{1}{2 \cdot sin 180^{\circ} / n} . \end{matrix}

(2)

Ezek után rátérhetünk a feladat fizikai részének megoldására. Merev testek nyugalmi állapotát akarjuk leírni, ennek pedig az a szükséges és elegendő feltétele, hogy a testekre ható erők eredője, valamint a forgatónyomatékok összege nulla legyen. Mivel a rendszer több testből áll, az egyensúly feltételének mindegyik testre külön‐külön teljesülnie kell.
Írjuk le először a középső golyó egyensúlyát (3. ábra).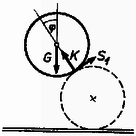

3. ábra

A testre

G

súlyerő, valamint ismeretlen nagyságú

K

nyomóerő és

S_{1}

súrlódási erő hat. Az utóbbi két erő természetesen

n

-szer lép fel, de csak egyet‐egyet tüntettünk fel a rajzon. Érdemes az erőket függőleges és vízszintes összetevőkre bontanunk.
A függőleges összetevők egyensúlyának feltétele :

\begin{matrix} G - n (K cos φ + S_{1} sin φ) = 0. \end{matrix}

(3)

A vízszintes összetevők eredője, valamint a forgatónyomatékok összege szimmet-ria‐okokból nyilván nulla.
Az asztallapon fekvő golyók mindegyikére a 4. ábrán látható erők hatnak.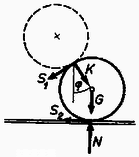

4. ábra

A nyomó- és súrlódási erők nagysága Newton III. axiómája értelmében megegyezik a 3. ábrán felvett erők nagyságával.

N

az asztal nyomóerejének,

S_{2}

az asztallap és a golyó közti súrlódási erőnek a nagyságát jelöli. Az alsó golyók nem hatnak egymásra semmilyen erővel, hiszen a legkisebb nyomóerő eltávolítaná őket egymástól, összeszorító erő hiányában viszont súrlódási erő sem léphet fel. Ismét felírhatjuk a függőleges és vízszintes erőkomponensek egyensúlyának feltételét :

\begin{matrix} K cos φ + S_{1} sin φ + G - N = 0, & (4) \\ K sin φ - S_{1} cos φ - S_{2} = 0. & (5) \end{matrix}

A forgatónyomatékok összege bármely pontra vonatkoztatva nulla kell, hogy legyen. A golyó középpontjára felírva :

\begin{matrix} S_{1} r - S_{2} r = 0. \end{matrix}

(6)

Vigyáznunk kell, a súrlódási erő és a nyomóerő között nem áll fenn az

F_{s} = μ F_{n y}

összefüggés, hiszen a testek nem csúsznak egymáson, hanem az

F_{s} ≦ μ

F_{n y}

egyenlőtlenség érvényes. Jelen esetben az egyensúly feltételéhez szükséges az

\begin{matrix} S_{1} ≦ K, és S_{2} ≦ μ \cdot N \end{matrix}

(7)

egyenlőtlenségek mindegyikének teljesülése.
A (3)‐(6) egyenletrendszer egyértelműen meghatározza az

S_{1}

S_{2}

K

és

N

ismeretleneket. A megoldás

\begin{matrix} N = \frac{n + 1}{n} G, K = \frac{1}{n} G, S_{1} = S_{2} = \frac{G}{n} \frac{sin φ}{1 + cos φ} . \end{matrix}

Ezeket (7)-be helyettesítve a

\begin{matrix} μ ≧ \frac{1}{n + 1} \frac{sin φ}{1 + cos φ}, \end{matrix}

(8)

illetve a

\begin{matrix} μ ≧ \frac{sin φ}{1 + cos φ} \end{matrix}

(9)

feltételeket kapjuk. Mivel (9) erősebb megszorítást jelent, mint (8), ezért az egyensúly szükséges és elégséges feltétele :

\begin{matrix} μ ≧ tg (φ / 2) . \end{matrix}

(10)

Az utolsó lépésnél felhasználtuk a

\begin{matrix} \frac{sin φ}{1 + cos φ} \equiv tg \frac{φ}{2} \end{matrix}

trigonometriai azonosságot. (2) alapján

sin φ

-t kifejezhetjük

n

-nel, így végül

n

darab golyónál a súrlódási együtthatóra alsó korlátként a

\begin{matrix} μ_{n} = 2 \cdot sin \frac{180^{\circ}}{n} - \sqrt[]{4 \cdot sin^{2} \frac{180^{\circ}}{n} - 1} \end{matrix}

(11)

kifejezést kapjuk. A megfelelő numerikus értékek

\begin{matrix} μ_{3} = \sqrt[]{3} - \sqrt[]{2} \approx 0, 32, μ_{4} = \sqrt[]{2} - 1 \approx 0, 41, μ_{5} \approx 0, 56. \end{matrix}

A (11) képlet formálisan érvényes

n = 2

és

n = 6

értékekre is. Az előbbi esetben

μ_{2} = 2 - \sqrt[]{3} = 0, 27

, de ilyenkor nincs értelme sokszögről beszélni és az egyensúly labilis.

n = 6

-ra

μ_{6} = 1

, ami csak akkor helyes, ha valamilyen módon biztosítani tudjuk, hogy a középső golyó ne támaszkodjék az asztalra ‐ hiszen ezt a számítás során kihasználtuk. Például a középső golyót egy nagyon kicsivel nagyobbra készíthetjük a többinél, vagy pedig egy kicsit horpadt felületre helyezzük a golyókat.

Ábrahám Tibor (Eger, Gárdonyi G. Gimn., II. o. t.) dolgozata alapján

II. megoldás. A feladatot megoldhatjuk szerkesztéssel is. Az asztalon levő bármely golyó akkor van egyensúlyban, ha a rá ható erők eredője nulla és hatásvonaluk egy ponton megy át. Ez utóbbi feltétel a forgatónyomatékok egyensúlyát biztosítja.
A

G

súlyerő, az asztal nyomóereje és az asztalnál fellépő súrlódási erő egyaránt a

B

ponton halad át (5. ábra).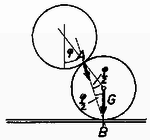

5. ábra

Szükséges tehát, hogy a felső golyó által kifejtett erő (nyomóerő

+

súrlódási erő), amelynek hatásvonala az

A

ponton biztosan átmegy, szintén a

B

ponton haladjon át. Ez annyit jelent, hogy az érintkezési felületre merőleges egyenes és az erő hatásvonala

φ / 2

szöget zár be. A (7) feltétel szerint viszont az egyensúly feltétele éppen az, hogy ezen szög tangense kisebb legyen, mint

μ

. Így közvetlenül megkaptuk (10) egyenlőtlenséget.

6. ábra

Az asztal és a golyó között ható erő a 6. ábra alapján biztosan kisebb szöget zár be a függőlegessel, mint

φ / 2

, ezért a (10) feltétel egyben azt is biztosítja, hogy az asztallapnál sem csúszhatnak meg a golyók.

Prőhle Péter (Bp., Fazekas M. Gyak. Gimn., II. o. t.)

Megjegyzés. A numerikus számítás eredményét összefoglaljuk a következő táblázatban :

\begin{matrix} n & T & sin φ & cos φ & μ \\ 2 & 30^{\circ} & \frac{1}{2} & \frac{\sqrt[]{3}}{2} & \frac{1}{2 + \sqrt[]{3}} = 0, 268 \\ 3 & 35, 2^{\circ} & \frac{\sqrt[]{3}}{3} & \sqrt[]{\frac{2}{3}} & \frac{1}{\sqrt[]{2} + \sqrt[]{3}} = 0, 318 \\ 4 & 45^{\circ} & \frac{\sqrt[]{2}}{2} & \frac{\sqrt[]{2}}{2} & \frac{1}{1 + \sqrt[]{2}} = \sqrt[]{2} - 1 = 0, 414 \\ 5 & 58, 7^{\circ} & \frac{2}{\sqrt[]{10 - 2 \sqrt[]{5}}} & \frac{\sqrt[]{5 - 2 \sqrt[]{5}}}{3} & \frac{2}{\sqrt[]{10 - 2 \sqrt[]{5}} + \sqrt[]{6 - 2 \sqrt[]{5}}} = 0, 559 \\ 6 & 90^{\circ} & 1 & 0 & 1   =1 \end{matrix}