Kezdőlap


Feladat:	966. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Éber Nándor
Füzet:	1971/november, 181 - 182. oldal		PDF \| MathML
Témakör(ök):	Pontszerű töltés térerőssége, Coulomb-törvény, Feladat
Hivatkozás(ok):	Feladatok: 1971/február: 966. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1) Két ponttöltés erőterének térerősségét a két töltéshez tartozó erőtér térerősségének vektori összegezésével kaphatjuk meg. A térerősség csak akkor lehet $0$ , ha a két töltéstől származó térerősség egyező nagyságú és ellentétes irányú. Mivel a Coulomb erő a töltést a ponttal összekötő egyenes mentén hat, ez csak a két töltést összekötő egyenesen, a két töltés ellenkező előjele miatt az összekötő szakaszon kívül, a kisebbikhez közelebb teljesülhet.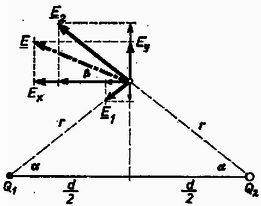

r

0

térerősségű pont

Q_{1}

től mért távolsága, akkor

\begin{matrix} k \frac{Q_{1}}{Q_{2}} + k \frac{Q_{2}}{{(r + d)}^{2}} = 0, innen \\ (Q_{1} + Q_{2}) r^{2} + 2 Q_{1} r d + Q_{1} d^{2} = 0, \\ r = \frac{- Q_{1} \pm \sqrt[]{- Q_{1} Q_{2}}}{Q_{1} + Q_{2}} d . \end{matrix}

Numerikusan

r_{1} = - 1 / 3

m, ill.

r_{2} = 1

m. Feltételünknek

r = 1

m felel meg. Azonos

Q_{1} = Q_{2} \neq 0

töltések esetén a térerősség ott

0

, ahol

\frac{Q}{r^{2}} - \frac{Q}{{(d - r)}^{2}} = 0

, ahonnan

r = d / 2 = 0, 5

m.
b) Ponttöltés potenciálja tőle

r

távolságban

k Q / r

, több töltésre szuperponálódik, így a potenciál ott

0

, ahol

\begin{matrix} \frac{Q_{1}}{r_{1}} + \frac{Q_{2}}{r_{2}} = 0, \frac{r_{1}}{r_{2}} = \frac{- Q_{1}}{Q_{2}} = \frac{1}{4}, \end{matrix}

ahol

r_{1}

, ill.

r_{2}

Q_{1}

, ill.

Q_{2}

-től mért távolság. Ez a feltétel egy Apollóniusz-gömböt határoz meg, mely a két töltést összekötő egyenest

Q_{1}

-től kifelé

1 / 3

Q_{2}

felé

1 / 5

m távolságra metszi, így középpontja

Q_{1}

-től kifelé

(\frac{1}{3} - \frac{1}{5}) \cdot \frac{1}{2} m=

= \frac{1}{15} m

-re van, sugara

(\frac{1}{3} + \frac{1}{5}) \cdot \frac{1}{2} m=\frac{4}{15}m

. (Az egyenesen levő pontok a)-hoz hasonlóan kaphatók.)
Ha

Q_{1} = Q_{2}

, akkor

Q_{1} / r_{1} + Q_{2} / r_{2}

mindkét tagja azonos előjelű, tehát sehol nem lehet

0

.
c) A probléma hengerszimmetriája miatt elegendő a potenciál és a térerősség változását egy, a két töltésen átmenő síkban vizsgálni.
A potenciál additivitása miatt a felező merőlegesen az összekötő egyenestől

x

távolságra a potenciál

\begin{matrix} U = \frac{k (Q_{1} + Q_{2})}{\sqrt[]{d^{2} / 4 + x^{2}}} = \frac{2 k (Q_{1} + Q_{2})}{d} cos α . \end{matrix}

Különböző töltések esetén

U = 9 \cdot 10^{9} {Nm}^{2} / C^{2} \cdot 3 \cdot 10^{- 8} C \cdot 2 cos α = 540 V \cdot cos α

, egyenlő töltések esetén

U = - 9 \cdot 10^{9} {Nm}^{2} / C^{2} \cdot 2 \cdot 10^{- 8} C \cdot 2 cos α = - 360 V \cdot cos α

.
Az eredő térerősség kiszámításához bontsuk föl a térerősséget derékszögű komponensekre. Ekkor

\begin{matrix} E_{x} = E_{2} cos α - E_{1} cos α = \frac{k (Q_{2} - Q_{1})}{r^{2}} cos α = \\ = \frac{k (Q_{2} - Q_{1}) 4}{d^{2}} cos^{3} α = 9 \cdot 10^{9} \frac{{Nm}^{2}}{C^{2}} \cdot \frac{(4 + 1) \cdot 10^{- 8} C \cdot 4 cos^{3} α}{1 m^{2}} = 1800 V/m \cdot cos^{3} α, \\ E_{y} = E_{1} sin α + E_{2} sin α = \frac{k (Q_{1} + Q_{2})}{r^{2}} sin α = \frac{k (Q_{1} + Q_{2}) 4}{d^{2}} cos^{2} α sin α = \\ = 9 \cdot 10^{9} \frac{{Nm}^{2}}{C^{2}} \cdot \frac{(4 - 1) 10^{- 8} C \cdot 4 \cdot cos^{2} α \cdot sin α}{1 m^{2}} = 1080 V/m \cdot cos^{2} α sin α \end{matrix}

Így a térerősség abszolút értéke

\begin{matrix} E = \sqrt[]{E_{x}^{2} + E_{y}^{2}} = \frac{4 k}{d^{2}} cos^{2} α \cdot \sqrt[]{{(Q_{2} - Q_{1})}^{2} cos^{2} α + {(Q_{1} + Q_{2})}^{2} sin^{2} α} = \\ = (4 k / d^{2}) cos^{2} α \cdot \sqrt[]{Q_{1}^{2} + Q_{2}^{2} - 2 Q_{1} Q_{2} cos 2 α} = 360 V/m \cdot cos^{2} α \cdot \sqrt[]{17 + 8 cos 2 α}, \end{matrix}

irányszögének tangense

\begin{matrix} tg β = \frac{E_{y}}{E_{x}} = \frac{Q_{2} + Q_{1}}{Q_{2} - Q_{1}} tg α = 0, 6 tg α . \end{matrix}

Q_{1} = Q_{2} = - 10^{- 8} C

, akkor

E_{x} = 0

E_{y} = E = \frac{8 k Q}{d^{2}} cos^{2} α sin α = - 720 V/m \cdot cos^{2} α sin α

,
vagyis a térerősség a

Q_{1} Q_{2}

szakasz felezőpontja felé irányul.

Éber Nándor (Bp., Móricz Zs. Gimn., III. o. t.)