Kezdőlap


Feladat:	936. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Dávid Gyula , Gnädig Péter , Iglói Ferenc , Sarbó János
Füzet:	1971/április, 185 - 187. oldal		PDF \| MathML
Témakör(ök):	Csúszásmentes (tiszta) gördülés, Egyéb merev test térbeli mozgása, Merev test impulzusnyomatéka (perdülete), Feladat
Hivatkozás(ok):	Feladatok: 1970/október: 936. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az érme egy merev test, melynek mozgását úgy írhatjuk le, hogy megadjuk minden időpillanatban súlypontjának sebességét és a súlypont körüli forgás szögsebességét. A megoldáshoz a következő lépések vezetnek:
1. Felírjuk a testre ható erőket és meghatározzuk a súlypontra vonatkoztatott forgatónyomatékokat (dinamikai változók).
2. Kiszámítjuk a test súlypontjának sebességét, a forgás szögsebességét és ezek időbeli változását (kinematikai változók).
3. A Newton-egyenletek alapján kapcsolatot teremtünk az erők és gyorsulások, illetve a forgatónyomatékok és a szögsebesség megváltozása (szöggyorsulás) között (a dinamika alapegyenletei).
4. Figyelembe vesszük, hogy az érme csúszásmentesen gördül, és ezért a kinematikai változók nem függetlenek egymástól (kényszerfeltételek).
5. Megoldjuk a kapott egyenletrendszert.
Ezek a lépések minden olyan feladatnál alkalmazhatók, ahol egy merev test mozgását kell leírnunk az erők ismeretében.

Nézzük meg, hogyan alakulnak a fenti lépések a jelen feladatnál!
1. Az érmére

m g

súlyerő, az asztallap

K

nyomóereje és

S

súrlódási erő hat (

1

. ábr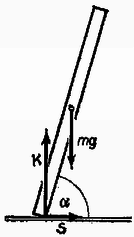a).

1. ábra

Ezen erők súlypontra vonatkoztatott forgatónyomatéka:

\begin{matrix} M = \sum_{i}^{} (r_{i} \times F_{i}), \end{matrix}

ahol

F

a testre ható erőket,

r_{i}

pedig a súlypontból az erők hatásvonalának tetszőleges pontjába mutató vektorokat jelöli (a vektoriális szorzás értelmezését l. a K. M. L.

1970

. évi

6

. számában közölt cikkben). A forgatónyomatékok nagysága

\begin{matrix} M = K r cos α - S r sin α, \end{matrix}

(1)

és iránya az erők síkjára merőleges (

2

. ábra).

2. ábra

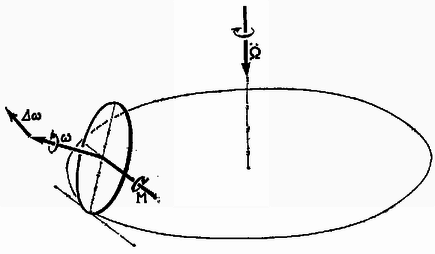2. Feltételezzük, hogy az érme egyenletes szögsebességgel gurul egy

R

sugarú körpályán. Jelöljük az érme súlypontjának szögsebességét

Ω

-val, a szimmetriatengely körüli forgás szögsebességét pedig

ω

-val (

2

. ábra). Ha

R ≫ r

, akkor a súlypont is jó közelítéssel

R

sugarú körpályán mozog és ezért a centripetális gyorsulás:

\begin{matrix} a = R Ω^{2} . \end{matrix}

(2)

Mivel

ω

-nak csak a nagysága állandó, iránya nem, ezért kérdezhetjük, hogy mennyit változik

ω

Δ t

idő alatt. Az érme

Δ t

idő alatt

Ω \cdot Δ t

szöggel fordul el, továbbá az

ω

vektor vízszintes vetülete

ω sin α

, ezért

\begin{matrix} | Δ ω | = Ω Δ t \cdot ω sin α . \end{matrix}

(3)

Δ ω

iránya megegyezik

M

irányával.
3. Newton II. törvénye alapján (felhasználva; hogy a függőleges gyorsulás nulla)

\begin{matrix} m g - K = 0, & (4) \\ S = m R Ω^{2} . & (5) \end{matrix}

A forgómozgás alapegyenlete szerint

\begin{matrix} Δ N = M Δ t, \end{matrix}

(6)

ahol

Δ N

az impulzusnyomaték megváltozása

Δ t

idő alatt (részletesebben l. az idézett cikket vagy Budó-Pócza: Kísérleti Fizika I. 49. §-t). Ha

R ≫ r

, akkor

Ω ≪ ω

, és az érme impulzusnyomatéka jó közelítésben csak az

ω

szögsebességből adódik. Felhasználjuk, hogy a henger tehetetlenségi nyomatéka

I = (1 / 2) m r^{2}

, továbbá

N = I ω

, ahonnan

\begin{matrix} Δ N = I Δ ω . \end{matrix}

(7)

4. A tiszta legördülés feltétele

\begin{matrix} r ω = R Ω . \end{matrix}

(8)

5. Az (1)‐(8) egyenleteket összevetve kapjuk, hogy

\begin{matrix} m \cdot g \cdot r \cdot cos α - S \cdot r \cdot sin α = (1 / 2) m \cdot r^{2} \cdot ω \cdot Ω \cdot sin α, \\ S = m R Ω^{2}, \\ R Ω = r ω . \end{matrix}

Az utóbbi három egyenlet megoldása:

\begin{matrix} \frac{R}{r} = \frac{3}{2} \frac{r ω^{2}}{g} tg α, & (9) \\ S = \frac{2}{3} \frac{m g}{tg α} . & (10) \end{matrix}

Ha megadjuk a kezdeti dőlésszöget és szögsebességet (vagy az energiát), akkor ezekből meghatározhatjuk a körpálya sugarát.
Ha a súrlódási együttható

μ

, akkor a tapadás (vagyis a tiszta legördülés) előfeltétele:

S \leq m g μ

, ahonnan

\begin{matrix} tg α \geq \frac{2}{3 μ} . \end{matrix}

(11)

Ha ennél laposabban indítjuk az érmét, akkor rögtön elcsúszik. Ha az érme veszít az energiájából, akkor

R

és

α

csökken mindaddig, amíg

(11)

-ben az egyenlőség nem teljesül. Ebből azonban csak a legkisebb dőlésszöget határozhatjuk meg, a minimális görbületi sugár kiszámítása csak az energiavesztés (légellenállás, gördülő súrlódás) részletes leírásával együtt lehetséges.

Összefoglalva: A pénzérme elfordulásának jelenségét a

(6)

egyenlet írja le. Ha egy merev testre ható forgatónyomaték forgástengely irányú, akkor a szögsebesség nagysága változik (szöggyorsulás), ha merőleges a forgástengelyre, akkor a forgástengely iránya változik (precesszió jelensége).
(4 pont)

Megjegyzés. Ha az

R ≫ r

feltétel nem teljesül, akkor

Ω

nem hanyagolható el

ω

mellett. Ilyenkor

Ω

-t fel kell bontani

ω

-val párhuzamos és arra merőleges összetevőkre és ezeket

I_{1}

, illetve

I_{2}

-vel szorozva kapjuk meg az eredő impulzusnyomatékot. Mivel a szimmetriatengelyre vonatkoztatott

I_{1}

és az egyik átmérőre vonatkoztatott

I_{2}

tehetetlenségi nyomaték nem egyezik meg egymással, ezért

N

iránya más lesz, mint

ω

iránya, és a

(7)

egyenletet módosítani kell. Egyébként a számítás menete hasonló a fentiekhez.

Gnädig Péter