Kezdőlap


Feladat:	902. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dombi Gábor , Sailer Kornél , Tél Katalin
Füzet:	1971/január, 36 - 38. oldal		PDF \| MathML
Témakör(ök):	Szabadesés, Tökéletesen rugalmatlan ütközések, Energiamegmaradás, Rugalmas energia, Harmonikus rezgőmozgás, Feladat
Hivatkozás(ok):	Feladatok: 1970/március: 902. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha a rugó felső végén nincs $M$ tömeg, akkor az egész folyamatra alkalmazhatjuk a mechanikai energia megmaradásának tételét. Mivel egy, nyugalmi helyzetéhez viszonyítva $h_{0}$ -lal megnyújtott vagy összenyomott rugó energiája 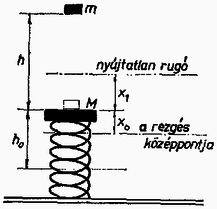$(1 / 2) D h_{0}^{2}$ , azért

\begin{matrix} (1 / 2) m v_{0}^{2} + m g (h + h_{0}) = (1 / 2) D h_{0}^{2}, \end{matrix}

tehát

\begin{matrix} v_{0} = \sqrt[]{\frac{D}{m} h_{0}^{2} - 2 g (h + h_{0})} \end{matrix}

függőleges kezdősebességgel kell elhajítani

m

-et, hogy a rugó

h_{0}

értékkel nyomja össze. Numerikus adatokkal

v_{0} \approx 12, 6

m/s.

Amennyiben a rugón

M

tömegű rugalmatlan teher nyugszik, akkor az

m

tömeg ezzel rugalmatlanul ütközik, tehát mechanikai energia hővé alakul. A mechanikai energia megmaradásának tételét így nem alkalmazhatjuk az egész folyamatra. Az ütközésig terjedő folyamatra

\begin{matrix} (1 / 2) m v_{0}^{2} + m g h = (1 / 2) m v^{2}, v = \sqrt[]{v_{0}^{2} + 2 g h}, \end{matrix}

ahol

v

a test ütközés előtti sebessége.

m

tömeg

M

-mel rugalmatlanul ütközik, az ütközés utáni közös

c

sebesség az impulzusmegmaradás tételéből

\begin{matrix} c = \frac{m v}{m + M} . \end{matrix}

Ütközés után a tömegek mozgási energiája

E_{m} = (1 / 2) (m + M) c^{2}

, a helyzeti energia megváltozása

E_{h} = (m + M) g h_{0}

. A rugó már az ütközés pillanatában is rendelkezett helyzeti energiával, mivel

M

súlyereje

x_{1} = M g / D

szakasszal nyomta össze. Így energiájának megváltozása

E_{r} = (1 / 2) D {(x_{1} + h_{0})}^{2} - (1 / 2) D x_{1}^{2}

.
A mechanikai energia megmaradásának tétele

\begin{matrix} E_{m} + E_{h} = E_{r}, \\ (1 / 2) (m + M) c^{2} + (m + M) g h_{0} = (1 / 2) D {(x_{1} + h_{0})}^{2} - (1 / 2) D x_{1}^{2} . \end{matrix}

Behelyettesítve

c

és

x_{1}

értékét

\begin{matrix} \frac{1}{2} \frac{m^{2}}{m + M} (v_{0}^{2} + 2 g h) + (m + M) g h_{0} = \frac{1}{2} D [{(\frac{M g}{D} + h_{0})}^{2} - {(\frac{M g}{D})}^{2}] . \end{matrix}

Innen

\begin{matrix} v_{0} = \sqrt[]{D \frac{m + M}{m^{2}} h_{0}^{2} - 2 \frac{m + M}{m^{2}} g h_{0} - 2 g h} . \end{matrix}

Numerikus értékekkel

v_{0} \approx 20, 1

m/s.

v_{0}

iránya egyaránt mutathat felfelé és lefelé, hiszen felfelé dobva el az

m

tömeget az eldobás helyén lefelé is

v_{0}

sebeséggel halad keresztül.

v_{0}

kifejezésének csak akkor van értelme, ha a négyzetgyök alatt nemnegatív szám áll, vagyis

\begin{matrix} D \frac{m + M}{m^{2}} h_{0}^{2} - 2 \frac{m + M}{m} g h_{0} - 2 g h \geq 0. \end{matrix}

Ha ez teljesül, akkor minden

v_{0}

esetén a rugó

h_{0}

-nál jobban összenyomódik. Az előbbi egyenlőtlenségből a rugó minimáliss összenyomódása

\begin{matrix} h_{0} \geq (g + \sqrt[]{g^{2} + 2 \frac{D g h}{m + M}}) \frac{m}{D} \approx 0, 06 m . \end{matrix}

Sailer Kornél (Ózd, József A. Gimn., IV. o. t.)

II. megoldás. Foglalkozzunk az általánosabb esettel, az

M = 0

-nak megfelelő speciális eset szolgáltatja az első eset megoldását.
Az

m

tömeg ütközés előtti sebessége a

v = v_{0} + g t

és

h = v_{0} t + (g / 2) t^{2}

összefüggésekből

t

kiküszöbölésével

v = \sqrt[]{v_{0}^{2} + 2 g h}

m

ekkora sebességgel rugalmatlanul ütközik az álló

M

-be, így ütközés utáni sebességük

\begin{matrix} c = \frac{m}{m + M} \sqrt[]{v_{0}^{2} + 2 g h} . \end{matrix}

Az ütközés után a mozgás egy harmonikus rezgőmozgás részének tekinthető, melynek középpontja az ütközés helye alatt

x_{0} = m g / D

távolsággal van, hiszen

m

súlyereje meg ennyivel nyomja össze a rugót. A rezgés amplitúdója

A =

= h_{0} - x_{0}

, körfrekvenciája

ω = \sqrt[]{\frac{D}{m + M}}

. A rezgés kitérése és sebessége idő függvényében

\begin{matrix} x = A sin (ω t + φ), v = A ω cos (ω t + φ) . \end{matrix}

m

tömeggel való ütközés helyén

\begin{matrix} x_{0} = A sin (ω t_{0} + φ), c = A ω cos (ω t_{0} + φ), \end{matrix}

innen

\begin{matrix} sin (ω t_{0} + φ) = x_{0} / A, cos (ω t_{0} + φ) = c / A ω . \end{matrix}

Mivel

sin^{2} α + cos^{2} α = 1

, ezért

\begin{matrix} {(\frac{x_{0}}{A})}^{2} + {(\frac{c}{A ω})}^{2} = 1, \end{matrix}

ahonnan

\begin{matrix} c^{2} = ω^{2} (A^{2} - x_{0}^{2}) = \frac{D}{m + M} [{(h_{0} - \frac{m g}{D})}^{2} - {(\frac{m g}{D})}^{2}] . \end{matrix}

Behelyettesítve

c

értékét

\begin{matrix} \frac{m^{2}}{{(m + M)}^{2}} (v_{0}^{2} + 2 g h) = \frac{D}{m + M} [{(h_{0} - \frac{m g}{D})}^{2} - {(\frac{m g}{D})}^{2}], \end{matrix}

ebből

\begin{matrix} v_{0} = \sqrt[]{D \frac{m + M}{m^{2}} h_{0}^{2} - 2 \frac{m + M}{m} g h_{0} - 2 g h}, \end{matrix}

ami megegyezik az első megoldás eredményével.

Tél Katalin (Bp., Apáczai Csere J. Gimn., III. o. t.)