Kezdőlap


Feladat:	878. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Berkes Enikő , Iglói Ferenc , Klebniczki József , Szolcsányi György , Turi Erzsébet
Füzet:	1970/november, 169 - 172. oldal		PDF \| MathML
Témakör(ök):	Kristályos anyagok, Analógia alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1969/december: 878. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $ϱ$ átlagsűrűség meghatározása visszavezethető az edényben levő golyók számának meghatározására. Ha ugyanis a $ϱ_{0}$ sűrűségű golyókból $N$ darab fér el a $V$ térfogatú edényben, akkor

\begin{matrix} \frac{4 R^{2} π}{3} N ϱ_{0} = ϱ V . \end{matrix}

(1)

Az edényben elhelyezhető golyók száma függ a golyók térbeli elrendeződésétől. Három jellegzetes elrendezéssel foglalkozunk.

I. Minden golyó

6

másikkal érintkezik. Az egy rétegben elhelyezkedő golyók középpontjai négyzethálózatot alkotnak és a következő rétegek golyói is pontosan e fölött helyezkednek el (1. ábra).

1. ábra

II. Minden golyónak

8

szomszédja van. Az egy réteghez tartozó golyók középpontjai rombuszhálózatot alkotnak és a következő réteg ismét pontosan az alatta levő fölé kerül (2. ábra).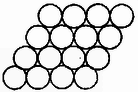

2. ábra

III. Minden golyó

12

másikkal érintkezik. Az egyes rétegek négyzethálós szerkezetűek, de a következő réteg golyói a szaggatott vonallal megjelölt helyekre kerülnek (3. ábra).

3. ábra

Ugyanennek az elrendezésnek másik nézete a 4. ábrán látható.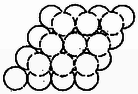

4. ábra

A fenti három elrendezés tetszőleges alakú edény középső részében megvalósítható, az edény falánál azonban a szabályos elrendeződés (az edény alakjától függő mértékben) elromlik.
Határozzuk meg az

m

magasságú hatszög alapú hasábban elhelyezhető golyók számát! A hatszög oldalélét az egyszerűség kedvéért vegyük

(2 k + \frac{2}{\sqrt[]{3}}) \cdot R

-nek, ekkor ugyanis egy oldalél mentén pontosan

k + 1

golyó fér el.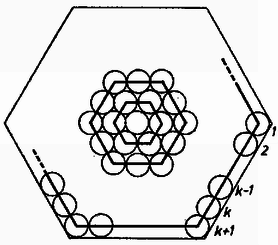

5. ábra

Számoljuk össze az 5. ábrán látható golyókat, melyek egy réteget alkotnak! A középponttól kiindulva hatszögenként leszámolhatjuk a golyókat:

\begin{matrix} n = 1 + 6 + 12 + ... + 6 k = 1 + 6 \frac{k (k + 1)}{2} = 3 k^{2} + 3 k + 1. \end{matrix}

Ha a II. elrendezést valósítjuk meg, akkor ugyanilyen rétegek ismétlődnek

[\frac{m}{2 R}]

-szer. (Az

[x]

jelölés az

x

szám egész részét jelenti.) Az edény térfogata

\begin{matrix} V = {(2 k + \frac{2}{\sqrt[]{3}})}^{2} R^{2} \cdot \frac{\sqrt[]{3}}{2} \cdot 3 m = 6 \sqrt[]{3} {(k + \frac{1}{\sqrt[]{3}})}^{2} R^{2} m . \end{matrix}

Az edényben levő golyók száma

N = (3 k^{2} + 3 k + 1) [\frac{m}{2 R}]

, így (1) felhasználásával

\begin{matrix} \frac{ϱ}{ϱ_{0}} = \frac{\frac{4 R^{3} π}{3} (3 k^{2} + 3 k + 1) [\frac{m}{2 R}]}{6 \sqrt[]{3} {(k + \frac{1}{\sqrt[]{3}})}^{2} R^{2} m} = \frac{1 + \frac{1}{k} + \frac{1}{3 k^{2}}}{{(1 + \frac{1}{k \sqrt[]{3}})}^{2}} \cdot \frac{[\frac{m}{2 R}]}{\frac{m}{2 R}} \cdot \frac{π}{3 \sqrt[]{3}} . \end{matrix}

(2)

A fenti eredmény három tényezőjének külön-külön szemléletes jelentése van. Az első tört értéke csak

k

-tól függ, és azt fejezi ki, hogy a hasáb palástjánál nem olyan jó a térkitöltés, mint a test belsejében. A tört értéke egynél mindig kisebb, de tetszés szerinti előírt pontossággal megközelíti azt, ha

k

elég nagy (pl:

k = 1

2

3

100

-ra a tört értéke

0, 93

;

0, 95

;

0,96

;

0, 998

).
A második tényező a sűrűségnek a magasságtól való függését írja le állandó

k

mellett, vagyis a d) kérdésre adja meg a választ. A 6. ábrán látható, hogy az

\frac{[x]}{x}

függvény értéke legfeljebb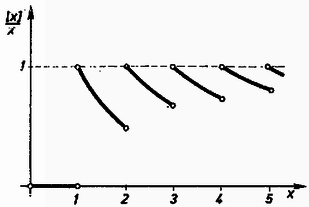

1

lehet.

6. ábra

m ≫ R

, vagyis ha sok réteg fér el az edényben, akkor elhanyagolhatjuk a legfelső réteg felett esetleg szabadon maradó helyet az edény térfogatához képest, azaz

\frac{2 R}{m} [\frac{m}{2 R}]

egynek vehető.
A harmadik tényező jellemzi a térkitöltés jóságát. Ha

k ≫ 1

és

m ≫ R

, akkor

\begin{matrix} ϱ = ϱ_{0} \cdot \frac{π}{3 \sqrt[]{3}} . \end{matrix}

(3)

Vizsgáljuk meg a III. elrendezést! A 4. ábrának megfelelően elhelyezett golyóknál minden második rétegbe csak

3 k^{2}

golyó fér el, viszont a rétegek távolsága egy

2 R

oldalélű tetraéder magassága, azaz

\frac{2 \sqrt[]{2}}{\sqrt[]{3}} R

. Az előző számoláshoz hasonlóan

\begin{matrix} \frac{ϱ}{ϱ_{0}} = \frac{\frac{4 R^{3} π}{3} \cdot \frac{(3 k^{2} + 3 k + 1) + 3 k^{2}}{2} {[\frac{m - 2 R}{2 \sqrt[]{2} R} \sqrt[]{3}] + 1}}{6 \sqrt[]{3} {(k + \frac{1}{\sqrt[]{3}})}^{2} R^{2} m} . \end{matrix}

(4)

m ≫ R

és

k ≫ 1

, akkor

\begin{matrix} ϱ = ϱ_{0} \cdot \frac{π}{6} \sqrt[]{2} . \end{matrix}

(5)

Vizsgáljuk meg az I. elrendezést négyzet alapú hasábra! Egy rétegbe

k^{2}

golyó fér el, a rétegek száma

[\frac{m}{2 R}]

az edény térfogata

{(2 k R)}^{2} m

, tehát

\begin{matrix} \frac{ϱ}{ϱ_{0}} = \frac{\frac{4 R^{3} π}{3} k^{2} \cdot [\frac{m}{2 R}]}{{(2 k R)}^{2} m} = \frac{[\frac{m}{2 R}]}{\frac{m}{2 R}} \cdot \frac{π}{6} . \end{matrix}

Érdekes, hogy most

k

-tól független a sűrűségek aránya. Ennek az az oka, hogy az edény alakja jól illeszkedik az elrendeződés négyzetes szimmetriájához és így a felületen sem rosszabb a térkitöltés, mint az edény belsejében. Hatszög alapú hasábra kiszámolva ugyanezt, ismét megjelenne egy

k

-tól függő egynél kisebb szorzótényező.
A fentiek alapján már valamennyi kérdésre választ tudunk adni.
a) Ha a golyók méretét

n

-ed részére csökkentjük, akkor valamennyi képletben

k

helyére

n \cdot k

-t,

R

helyébe

\frac{R}{n}

-t kell írni. Az átlagsűrűség változását a II. elrendezésnél (2) írja le. A golyók méretét csökkentve belátható, hogy az első tényező biztosan növekszik. A második tényező sem csökkenhet, hiszen érvényes az

[n x] \geq n [x]

egyenlőtlenség. Tehát az átlagsűrűség növekszik, de ez a növekedés

k ≫ 1

m ≫ R

esetben elhanyagolhatóan kicsi.
b) A fém sűrűségét

k

m

értékének, valamint az elrendeződés jellegének ismeretében lehet meghatározni. Ha

k ≫ 1

és

m ≫ R

, akkor a három elrendeződésnél (az edény alakjától függetlenül) rendre

\begin{matrix} I. ϱ_{0} = \frac{6}{π} ϱ = 13 {g/cm}^{3}; & II. ϱ_{0} = \frac{3 \sqrt[]{3}}{π} ϱ = 11, 2 {g/cm}^{3}; \\ III. ϱ_{0} = \frac{3 \sqrt[]{2}}{π} ϱ = 9, 2 {g/cm}^{3} . \end{matrix}

c) Ha

k ≫ 1

és

m ≫ R

, akkor a térkitöltés jóságát a

π / 6

(π / 3) \sqrt[]{3}

és

(π / 6) \sqrt[]{2}

számok jellemzik. A legjobb térkitöltést a III. elrendezés adja. Ha a golyók száma kicsi, akkor a felület közelében található hibák hatása jelentős és a legkedvezőbb térkitöltést az edény alakjához legjobban illeszkedő elrendezés adja. Ez hatszög alapú hasábnál a II., négyzet alapú hasábnál az I. elrendezés. Azt a

k

értéket, amelyiknél a legsűrűbb térkitöltés elrendeződés-változást igényel, a (2), illetve (4) típusú kifejezésekből lehet meghatározni.

Megjegyzés. A kitűzésben

(2 k + 1) R

oldalélű hatszög szerepelt. Ezt nem lehet szorosan kirakni golyókkal, ezért számoltunk más értékkel. Az ebből adódó eltérések a megoldás lényegét nem érintik és így az elért pontokat nem változtatták meg.