Kezdőlap


Feladat:	768. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Fischer Ágnes , Gerhardt Tamás , Gyimesi Ferenc , Hordósy Gábor , Láz József , Sailer Kornél , Szamosújvári Sándor
Füzet:	1969/január, 44 - 45. oldal		PDF \| MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei, Feladat
Hivatkozás(ok):	Feladatok: 1968/május: 768. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Oldjuk meg a feladatot általánosan! Jelöljük a tömegeket az ábra szerint $m_{1}$ , $m_{2}$ , $m_{3}$ , $m$ és $x$ -szel, a csigák gyorsulását $a$ -va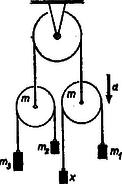l!

1. ábra

Határozzuk meg a kötélerőket! Ha a mozgó csigához képest az

m_{1}

és

x

tömegű testek

A

gyorsulással mozognak, akkor a három testre a következő mozgásegyenletek írhatók fel:

\begin{matrix} m_{1} g - K_{1} = m_{1} (a + A), & (1) \\ x g - K_{1} = x (a - A), & (2) \\ m g + 2 K_{1} - K_{2} = m a . & (3) \end{matrix}

(1) és (2)-t

x

-szel, illetve

m_{1}

-gyel szorozva és összeadva kapjuk, hogy

\begin{matrix} 2 m_{1} x g - x K_{1} - m_{1} K_{1} = 2 m_{1} x a, ahonnan \\ K_{1} = \frac{2 m_{1} x}{m_{1} + x} (g - a) . & (4) \end{matrix}

Ezt (3)-ba behelyettesítve és

K_{2}

-t kifejezve:

\begin{matrix} K_{2} = \frac{4 m_{1} x}{m_{1} + x} (g - a) + m (g - a) . \end{matrix}

(5)

Teljesen hasonlóan határozhatjuk meg a másik mozgócsigánál fellépő kötélerőt, csak ott

a

ellentétes irányú: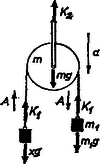

\begin{matrix} K'_{2} = \frac{4 m_{2} m_{3}}{m_{2} + m_{3}} (g + a) + m (g + a) . \end{matrix}

Ugyanazon kötél két végén a kötélerő megegyezik, tehát

K_{2} = K'_{2}

2. ábra

Részletesen kiírva

\begin{matrix} \frac{4 m_{1} x}{m_{1} + x} (g - a) + m (g - a) = \frac{4 m_{2} m_{3}}{m_{2} + m_{3}} (g + a) + m (g + a) . \end{matrix}

(6)

Az egyenletet

x

-re megoldva a következő kifejezést kapjuk:

\begin{matrix} x = \frac{2 m_{1} m_{2} m_{3} g + (2 m_{1} m_{2} m_{3} + m m_{1} m_{2} + m m_{1} m_{3}) a}{2 (m_{1} m_{2} + m_{1} m_{3} - m_{2} m_{3}) g - (2 m_{2} m_{3} + m m_{2} + m m_{3} + 2 m_{1} m_{2} + 2 m_{1} m_{3}) a} . \end{matrix}

(7)

Ezek után mindhárom kérdésre válaszolhatunk.
a) Ha a csigák nem mozognak (

a = 0

), akkor

\begin{matrix} x = \frac{m_{1} m_{2} m_{3}}{m_{1} m_{2} + m_{1} m_{3} - m_{2} m_{3}} . \end{matrix}

(8)

Behelyettesítve az

m_{1} = m

m_{2} = 2 m

és

m_{3} = 3 m

értékeket,

x = - 6 m

eredményt kapjunk. Ez fizikailag nem reális, mivel tömeg csak pozitív lehet.
c)

x

-re akkor kapunk pozitív értéket, ha (8)-ban a nevező pozitív, vagyis ha

m_{1} m_{2} + m_{1} m_{3} - m_{2} m_{3} > 0

. Átrendezéssel

\frac{1}{m_{1}} < \frac{1}{m_{2}} + \frac{1}{m_{3}}

. Ez a feltétel a) esetben nem teljesült.
b) Ha (7)-be beírjuk a megfelelő tömegértékeket, akkor

\begin{matrix} x = \frac{- 12 g - 17 a}{2 g + 27 a} m értéket kapunk . \end{matrix}

(9)

Ezzel

a = 1 {m/s}^{2}

mellett negatív. A feladat szövegében nem szerepel

a

gyorsulás iránya, így

a

lehet

- 1 {m/s}^{2}

is. Ekkor

x = 13, 6 m

Hordósy Gábor (Győr, Czuczor G. Gimn., III. o. t.) és Láz József (Bp., Eötvös J. Gimn., II. o. t.) dolgozata alapján

Megjegyzés. A megoldásnál nem vettük figyelembe a csigák forgását.

Gyimesi Ferenc (Győr, Révai M. Gimn., II. o. t.)