Kezdőlap


Feladat:	664. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bálványos Zoltán , Breuer Pál , Büttner György , Sághy András
Füzet:	1967/november, 174 - 175. oldal		PDF \| MathML
Témakör(ök):	Rugalmatlan ütközések, Feladat
Hivatkozás(ok):	Feladatok: 1967/február: 664. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Oldjuk meg a problémát rögtön általánosan. Felírhatjuk az impulzus-megmaradás törvényét és $ε$ definíciójából a relatív sebességek arányát.
Ez két egyenlet az $u_{1}$ és $u_{2}$ ismeretlenekre.

\begin{matrix} m_{1} v_{1} + m_{2} v_{2} = m_{1} u_{1} + m_{2} u_{2} & (1) \\ illetve ε = \frac{u_{1} - u_{2}}{v_{2} - v_{1}} . & (2) \end{matrix}

(2)-ből

u_{1} = ε (v_{2} - v_{1}) + u_{2}

, behelyettesítve (1)-be és

u_{2}

értékét kifejezve

\begin{matrix} u_{2} = \frac{m_{1} v_{1} (1 + ε) + (m_{2} - ε m_{1}) v_{2}}{m_{1} + m_{2}}, hasonlóan \\ u_{1} = \frac{(m_{1} - ε m_{2}) v_{1} + m_{2} v_{2} (1 + ε)}{m_{1} + m_{2}} . & (3) \end{matrix}

Numerikus adatokat behelyettesítve kapjuk

u_{1}

és

u_{2}

értékét mint

ε

függvényét:

u_{1} = 3 (1 - ε) m/s

és

u_{2} = (5 ε + 3) m/s

. Ábrázoljuk ezt grafikusan.

ε

értéke nyilván

1

és

0

között változhat (1. ábra).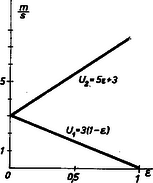

1. ábra

ε

nő, akkor

u_{2}

értéke is nő, míg

u_{1}

értéke csökken, de mindig pozitív marad, azaz mindkét golyó az ütközés után minden esetben az

m_{1}

eredeti haladási irányába fog haladni. Teljesen rugalmatlan ütközés esetén

(ε = 0)

mindkét golyó sebessége

u_{1} = u_{2} = 3 m/s

, míg teljesen rugalmas esetben

(ε = 1)

u_{2} = 8 m/s

, és

u_{1} = 0

, azaz az első golyó nyugalomban marad.
b) Ahhoz, hogy

u_{1} = 0

legyen, (3) alapján szükséges, hogy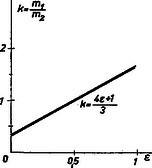

\begin{matrix} m_{1} v_{1} (1 + ε) + (m_{2} - ε m_{1}) v_{2} = 0, \end{matrix}

azaz

\begin{matrix} \frac{m_{1}}{m_{2}} = k = \frac{ε (v_{1} - v_{2}) - v_{2}}{v_{1}} \end{matrix}

teljesüljön. Adatainkkal

k = (4 ε + 1) / 3

k = 1 / 3

, ha

ε = 0

, és

k = 5 / 3

, ha

ε = 1

, mint azt már az előzőekben láttuk (2. ábra). Érdekes, hogy a kívánt feltétel teljesüléséhez

k

csak ily szűk határok közt változhat (ezen kezdeti sebességek mellett).

2. ábra

Bálványos Zoltán (Makó, József A. g. II. o. t.)

Megjegyzés. Csak a teljesen rugalmas ütközés esetén érvényes a mechanikai energia megmaradásának törvénye. Az elveszett energia nyilván

Δ E = (m_{1} v_{1}^{2} +

+ m_{2} v_{2}^{2} - m_{1} u_{1}^{2} - m_{2} u_{2}^{2}) / 2

u_{1}

és

u_{2}

értékét behelyettesítve

\begin{matrix} Δ E = \frac{m_{1} m_{2} {(v_{1} - v_{2})}^{2} (1 - ε^{2})}{2 (m_{1} + m_{2})} . \end{matrix}

Látható, hogy ez a teljesen rugalmas ütközéskor

0

, míg a rugalmatlan ütközésnél a legnagyobb.

Büttner György (Esztergom, I. István g. II. o. t.)