Kezdőlap


Feladat:	167. fizika mérési feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Major Zsuzsanna
Füzet:	1995/október, 442 - 445. oldal		PDF \| MathML
Témakör(ök):	Mechanikai mérés, Kötélsúrlódás, Mérési feladat
Hivatkozás(ok):	Feladatok: 1995/január: 167. fizika mérési feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy spárgadarab és valamilyen fémfelület közötti csúszási, ill. tapadási tényező meghatározására a megoldók igen sok egyszerű, mégis ötletes módszert használtak. Tekintsük át először a különböző módszerek elvi lényegét!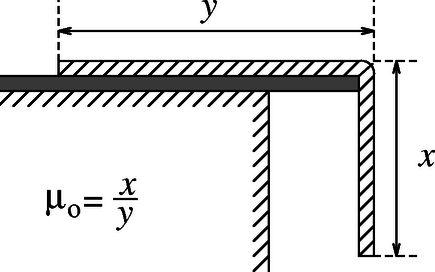
$a)$ ,,Lógatásos módszer.'' Ez talán a legegyszerűbb módszer a tapadási súrlódási együttható meghatározására. Egy darab spárgát az 1. ábrán látható módon fektessünk rá egy vízszintes fémfelületre úgy, hogy a felület szélénél a spárga egy része lelógjon. Növeljük addig a lelógó rész hosszát, amíg a madzag éppen meg nem csúszik. Feltételezve, hogy a spárga tömegeloszlása homogén, és hogy a lap élénél a kötélerő nem változik ugrásszerűen, a tapadási súrlódási együttható a lelógó és az asztalon fekvő kötéldarabok hosszainak hányadosaként kapható meg. (Valóban, az asztalon fekvő kötélrészre ható nyomóerő megegyezik ennek a kötéldarabnak a súlyával, míg az erre a részre az élnél ható vízszintes húzóerő (amellyel a tapadási súrlódási erő tart egyensúlyt) megegyezik a lelógó rész súlyával.) A $d)$ pontban, a ,,tekeréses módszer'' vizsgálatánál látni fogjuk, hogy az élnél a kötelet feszítő erő ugrásszerűen változik, a vízszintes irányú erő $e^{- μ_{0} π / 2}$ -szerese a függőleges irányú erőnek. ( $μ_{0}$ a tapadási súrlódási együttható.) Ezt az ugrást csak kis $μ_{0}$ értékek mellett hanyagolhatjuk el.

1. ábra

b)

,,Direkt módszer.'' E módszer közvetlenül a csúszási, ill. tapadási együttható definícióját használja föl. Helyezzünk ismert súlyú, spárgával ,,bevont'' testet (vagy spárga-gombolyagot) vízszintes fémfelületre, és mérjük meg a test nyugalomból való kimozdításához, ill. egyenletes sebességgel való mozgatásához szükséges vízszintes húzóerőt. A húzóerők és a súly hányadosa megadja a súrlódási együtthatókat. (Természetesen a mérést végezhetjük fordított elrendezésben is: a vízszintes felületet vonjuk be spárgával, és ezen húzunk egy fém testet. A mérést úgy is elvégezhetjük, hogy két ismert erővel egymáshoz szorított fémlap között húzzuk a madzagot.)

c)

,,Lejtős módszer.'' Spárgával bevont testet helyezzünk sima, változtatható hajlásszögű fém lejtőre (2. ábra). A lejtő hajlásszögét lassan növeljük addig, amíg a test éppen meg nem csúszik. Jelölje ezt a kritikus dőlésszöget

α_{0}

, a test tömegét pedig

m

. Ebben a helyzetben a

μ_{0} m g cos α_{0}

nagyságú, a lejtővel párhuzamos irányú tapadási súrlódási erő tart egyensúlyt a nehézségi erő

m g sin α_{0}

nagyságú, lejtő irányú komponensével, így a tapadási súrlódási együttható

μ_{0} = tg α_{0}

. A csúszási súrlódási együttható annak a hajlásszögnek a tangensével egyezik meg, amely mellett a testet kicsit megpöckölve az egyenletesen (nem gyorsulva) csúszik le a lejtőn.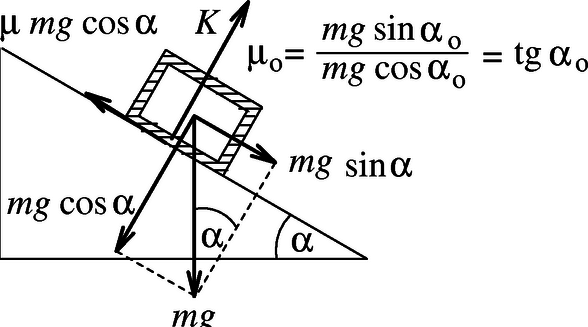

2. ábra

d)

,,Tekercseléses módszer.'' A módszer lényege az, hogy a spárgát ismert

φ

szögben rátekerjük egy sima, kör keresztmetszetű fémrúdra, és megmérjük, hogy a spárga egyik végét ismert erővel húzva mekkora erőt kell kifejtenünk a spárga másik végén ahhoz, hogy az éppen ne mozduljon el, ill. hogy állandó sebességgel csússzon (3. ábra). A megfeszített madzag rászorul a hengeres fémrúdra, a felcsavart kötélszakasz mentén tapadási, ill. csúszási súrlódási erő lép fel, amely megegyezik a kötél két végénél ható erők különbségével. Vizsgáljuk meg, hogy hogyan változik a kötélben az

F (φ)

feszítőerő a

φ

felcsavarodási szög függvényében! A 4. ábra a felcsavart kötél egy kis

Δ φ

szöghöz tartozó szakaszát mutatja kinagyítva. Látható, hogy e kis szakasz két végénél ható

F (φ)

, ill.

F (φ + Δ φ)

nagyságú erő sugárirányú komponenseinek összege

\begin{matrix} Δ N (φ) = sin (\frac{Δ φ}{2}) (F (φ) + F (φ + Δ φ)) \approx \frac{Δ φ}{2} (F (φ) + F (φ)) = Δ φ F (φ), \end{matrix}

míg az érintő irányú komponensek összege

\begin{matrix} Δ T (φ) = cos (\frac{Δ φ}{2}) (F (φ) - F (φ + Δ φ)) \approx - (F (φ + Δ φ) - F (φ)) . \end{matrix}

E két mennyiség hányadosa éppen a súrlódási együttható, így az

F

függvényre kis

Δ φ

esetén teljesül, hogy

\begin{matrix} \frac{F (φ + Δ φ) - F (φ)}{Δ φ} = - μ F (φ) . \end{matrix}

Ismeretes, hogy az ilyen tulajdonságú függvények az exponenciális függvények, azaz

\begin{matrix} F (φ) = F (0) e^{- μ φ}, \end{matrix}

(*)

tehát a felcsavart kötélben a feszítőerő a rúd sugarától függetlenül a szöggel exponenciálisan csökken. Az

a)

pontban a ,,lógatásos módszernél'' az él hatása tekinthető úgy, mintha a spárga nagyon kis sugarú,

π / 2

szögű körívre lenne ráfektetve, így a kötélerő az élnél valóban az

e^{- μ_{0} π / 2}

-szeresére csökken.

3. ábra

4. ábra

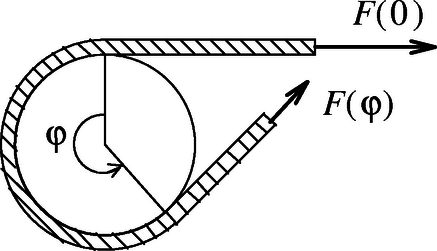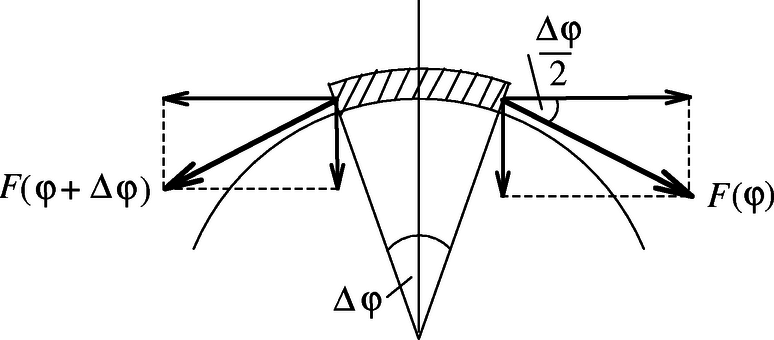Major Zsuzsanna (Stuttgart, Friedrich-Eugens Gymnasium, III. o.t.) mérését a fenti módszerrel végezte. Fémrúdra néhányszor rátekert madzag két végénél mérte a kötélerőt úgy, hogy a madzag még éppen nem csúszott meg (tapadási súrlódási együttható mérése), ill. úgy, hogy a kötél egyenletes sebességgel csúszott (csúszási súrlódási együttható mérése). A

(*)

összefüggésből látható, hogy

ln (\frac{F (0)}{F (φ)}) = μ φ

, így a két kötélvégen ható erő hányadosának logaritmusát ábrázolva a feltekercselés szögének függvényében egyenest kapunk, amelynek meredeksége éppen a keresett súrlódási együttható. Ezen egyenesek láthatók az 1., ill. 2. grafikonon. A mért csúszási együttható

μ = 0, 21 \pm 0, 03

, a mért tapadási súrlódási együttható pedig

μ_{0} = 0, 18 \pm 0, 015

. (Más minőségű anyagpárok esetén természetesen ettől eltérő értékek is kijöhetnek.) Meglepő módon a tapadási súrlódási együttható mért értéke kisebb, mint a csúszási súrlódási együtthatóé, ezt valószínűleg a csúszási súrlódási együttható sebességfüggése okozza.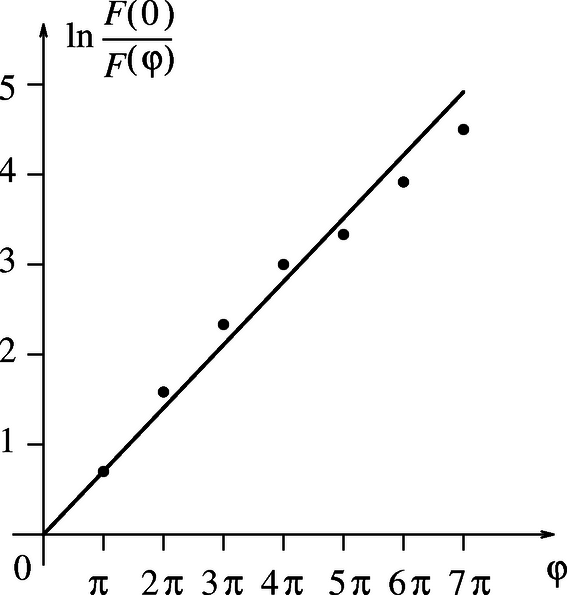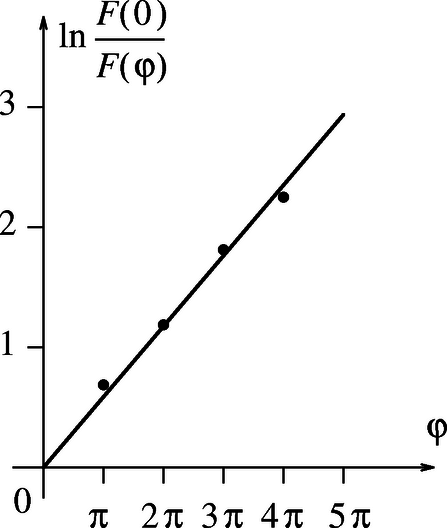

1. grafikon. A csúszási súrlódás mérése

2. grafikon. A tapadási súrlódás mérése