Kezdőlap


Feladat:	64. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Jorga Gergely
Füzet:	1894/június, 55 - 56. oldal		PDF \| MathML
Témakör(ök):	Euler-egyenes, Sokszögek súlypontjának koordinátái, Egyenesek egyenlete, Osztópontok koordinátái, Súlypont, Magasságpont, Körülírt kör középpontja, Elsőfokú (és arra visszavezethető) egyenletrendszerek, Feladat
Hivatkozás(ok):	Feladatok: 1894/május: 64. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $O M N$ háromszög súlypontját nyerem, ha az $N$ és $M$ pontokat összekötöm az $O M$ és $O N$ egyenesek felezési pontjaival $N'$ és $M'$ -tel. Az $N N'$ és $M M'$ egyenesek metszéspontja $G$ a keresett súlypont. Fel kell tehát írnom ezen utóbbi egyenesek egyenleteit. E végből ismernem kell az $N'$ és $M'$ pontok koordinátáit. De ezek a következők:

\begin{matrix} N' (\frac{0 + 10}{2}, \frac{0 + 0}{2}) = N' (5,0), \end{matrix}

\begin{matrix} M' (\frac{0 + 6}{2}, \frac{0 + 8}{2}) = M' (3,4) . \end{matrix}

Ennélfogva az

N N'

és

M M'

egyenesek egyenletei:

\begin{matrix} N N' ... y - 0 = \frac{0 - 8}{5 - 6} (x - 5) \end{matrix}

\begin{matrix} y = 8 (x - 5) \end{matrix}

\begin{matrix} y - 8 x + 40 = 0 \end{matrix}

\begin{matrix} M M' ... y - 0 = \frac{0 - 4}{10 - 3} (x - 10) \end{matrix}

\begin{matrix} 7 y = - 4 x + 40 \end{matrix}

\begin{matrix} 7 y + 4 x - 40 = 0 \end{matrix}

Az 1) és 2) egyenletekből kiszámíthatók a

G

pont koordinátáinak mérőszámai.

\begin{matrix} G (\frac{16}{3}, \frac{8}{3}) . \end{matrix}

A három magasságvonal átmenési pontját

H

-t megkapom, ha az

N

és

M

pontokból a szemben fekvő egyenesekre merőlegeseket húzunk és e merőlegesek metszéspontját felkeressük. Az

O M

és

O N

egyenesek egyenletei azonban a következők:

\begin{matrix} O M ... y = 0, \end{matrix}

\begin{matrix} O N ... 6 y - 8 x = 0 \end{matrix}

Tehát a reájuk merőleges

N N''

és

M M''

egyenesek egyenletei:

\begin{matrix} N N'' ... x = 6 \end{matrix}

\begin{matrix} M M'' ... 8 y + 6 x - 60 = 0 \end{matrix}

és így a

H

pont koordinátái:

H (6,3) .

Végre a háromszög körül írható kör középpontját

C

-t megkapom, ha az

N'

és

M'

pontokban az

O M

és

O N

egyenesekre merőlegeseket emelek és ez egyenesek metszéspontjait felkeresem. De az

N' C

és

M' C

egyenesek egyenletei a következők:

\begin{matrix} N C ... x = 5 \end{matrix}

\begin{matrix} M C ... 8 y + 6 x - 50 = 0 \end{matrix}

és így a

C

pont koordinátái:

\begin{matrix} C (5, \frac{5}{2}) \end{matrix}

Ha három pont koordinátáit általánosságban

x_{k}

és

y_{k}

-val jeleljük, hol

k = 1, 2, 3

-mal, annak feltételét, hogy a három pont egy egyenesben fekszik, a következő egyenlet fejezi ki:

\begin{matrix} x_{1} (y_{2} - y_{3}) + x_{2} (y_{2} - y_{1}) + x_{3} (y_{1} - y_{2}) = 0 \end{matrix}

Tehát a jelen esetben:

\begin{matrix} \frac{16}{3} (3 - \frac{5}{2}) + 6 (\frac{5}{2} - \frac{8}{3}) = 0 \end{matrix}

\begin{matrix} 16 + 15 + \frac{40}{3} - 16 - 15 = 0 \end{matrix}

Ez utóbbi egyenlet szemmel láthatólag identitás. Hogy végre

C H = 3 C G

-vel azt közvetlenül bebizonyíthatom, ha felírom

C H

és

C G

értékeit a

C, G

és

H

pontok koordinátáinak segélyével; ekkor ugyanis:

\begin{matrix} C H^{2} = {(5 - 6)}^{2} + {(\frac{5}{2} - 3)}^{2} = \frac{5}{4} \end{matrix}

és

\begin{matrix} C G^{2} = {(5 - \frac{16}{3})}^{2} + (\frac{5}{2} - {\frac{8}{3}}^{2}) = \frac{1}{9} + \frac{1}{36} = \frac{5}{36} \end{matrix}

Tehát

\begin{matrix} C H^{2} = 9 C G^{2}, \end{matrix}

és

\begin{matrix} C H = 3 C G . \end{matrix}

A mi bebizonyítandó volt.
(Jorga Gergely, főreálisk. VIII. oszt. tanuló, Arad)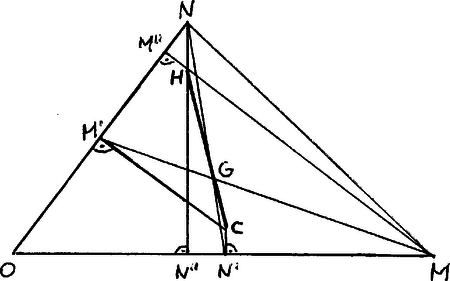

10. ábra

Jegyzet. Hogy a

C G H

pontok egy egyenesben feküsznek és a

C H = 3 C G

-vel, az a 10. ábrából a planimetria tételeivel is egyszerűen kimutatható.
Kösszük össze az

M'

és

N'

pontokat egy egyenessel. A

G N' M'

és

H N M

háromszögek hasonlóságából következik, hogy:

\begin{matrix} \frac{C N'}{N H} = \frac{N' M'}{M N} = \frac{1}{2} \end{matrix}

Nevezzük a

C H

és

N N'

egyenesek metszéspontját

G'

-nek, akkor a

C G' H

és

H G' N

háromszögek hasonlóságából következik, hogy:

\begin{matrix} \frac{C G'}{H G'} = \frac{N' G'}{N G'} = \frac{C N'}{H N} = \frac{1}{2} \end{matrix}

De a háromszög súlypontja

G

N N'

és

M M'

egyenesek metszéspontja és a

G N' M'

és

G N M

háromszögek hasonlóságából következik, hogy

\begin{matrix} \frac{N' G}{N G} = \frac{M' G}{M G} = \frac{N' M'}{N M} = \frac{1}{2} \end{matrix}

A 2) és 3) egyenlet összehasonlításából folyik, hogy

\begin{matrix} \frac{N' G'}{N G'} = \frac{N' G}{N G}, \end{matrix}

azaz a

G'

és

G

pontok azonosak, vagyis a

C G H

pontok egy egyenesben feküsznek; továbbá a 2)-ből

2 C G = H G, 3 C G = H G + C G = C H,

vagyis a

C H

C G

háromszorosa.