Feladat: 1988. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bíró András ,  Csirik János ,  Fleiner Tamás ,  Hausel Tamás ,  Mándy Attila ,  Pásztor Gábor ,  Sustik Mátyás 
Füzet: 1989/február, 56 - 60. oldal  PDF  |  MathML 
Témakör(ök): Négyszögek geometriája, Háromszögek nevezetes tételei, Négyzetrács geometriája, Egyéb sokszögek geometriája, Paralelogrammák, Helyvektorok, Ponthalmazok, Középpontos tükrözés, Magasságvonal, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1989/február: 1988. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Hogy rövidebben tudjuk magunkat kifejezni, az egész koordinátájú pontokat rácspontnak fogjuk nevezni és az olyan sokszögeket, amelyeknek minden csúcsa rácspont, rácssokszögnek.

 

I. megoldás. 1. Egyrészt belátjuk, hogy a sokszög, pontosabban a PQR vagy a PQS háromszög tartalmaz a csúcsain kívül is rácspontot, másrészt azt, hogy ha van rácspont az EPS vagy az EQR háromszög belsejében, akkor egy ilyen rácsponttal helyettesítve az S, illetőleg az R csúcsot, elég az állítást a keletkező kisebb négyszögre bizonyítani, erre is teljesülnek a feladat feltételei.
A kettőből következik a feladat állítása. Négyszögünk ugyanis csak véges számú rácspontot tartalmazhat, így a második állításban megfogalmazott eljárást véges sokszor alkalmazva, ha szükséges, olyan négyszöghöz jutunk, amelyikben a (megfelelő) EPS és EQR háromszög belsejében már nincs rácspont. Az első állítás szerint ebben is tartalmaz rácspontot a csúcsain kívül a PQR vagy a PQS háromszög. Ezt a rácspontot tehát az EPQ háromszögnek is tartalmaznia kell, és különbözik P-től és Q-tól.
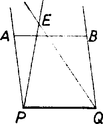
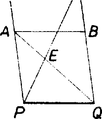
2. A fenti második állítás helyessége nyilvánvaló. Ha ugyanis pl. az EQR háromszögben van egy T rácspont (7. ábra), akkor TQP∢<RQP∢, tehát a szögekre vonatkozó feltétel a PQTS négyszögre is teljesül; az átlók E' metszéspontja pedig a QS átló QE szakaszára esik, tehát az E'PQ háromszögben levő rácspont az EPQ háromszögnek is pontja.
 
 
7. ábra
 

3. Válasszuk a betűzést úgy, hogy az R csúcs ne essék közelebb a PQ egyeneshez, mint S. Ekkor az a T pont, amelyikre PTRS paralelogramma, a PQR háromszög belsejében van, vagy a PQ szakasz belsejében, mert a szögfeltétel szerint az RT félegyenes a négyszög belseje felé indul, a PT félegyenes pedig vagy a négyszög belsejébe indul, vagy egybeesik a PQ félegyenessel.
T rácspont. Jelöljük ugyanis a P, R, S, T koordinátáit (p1,p2), (r1,r2), (s1,s2), (t1,t2)-vel. A paralelogramma átlóinak felezőpontjai egybeesnek. Ezt koordinátákban felírva
p1+r12=t1+s12,p2+r22=t2+s22.
Innen a T pont koordinátái
ti=pi+ri-si(i=1,2).
Ezek egész számok, ha pi,ri,si egész. Ezzel az 1. rész első állítását is igazoltuk, a feladatot megoldottuk.
 

Megjegyzések: 1. A 3. pontban lényegében a következő tételt bizonyítottuk be, amelyik független a rácspontoktól: Minden konvex négyszögnek van olyan csúcsa, amelyikből induló oldalakat paralelogrammává egészítve ki, ezt a négyszög tartalmazza. Ez az 1950. évben a Középiskolai Matematikai Lapok Országos Tanulóversenyén (a mai Arany Dániel verseny elődje) a haladók 3. feladata volt.*
A tétel speciális esete a következőnek: Egy konvex n-szögnek, ha n>3, legalább n-3 olyan csúcsa van, amelyekből induló oldalakat paralelogrammává egészítve ki, a paralelogrammát a sokszög tartalmazza. Ez viszont már az egyetemi hallgatók 1964. évi Schweitzer Miklós emlékversenyének 4. feladata volt.*
2. A harmadik pont második állítása így fogalmazható: Egy rácspontnak két rácspont közti szakasz felezőpontjára vonatkozó tükörképe rácspont. Ez igaz egységnyi oldalú négyzetekből épített rács helyett tetszés szerinti paralelogrammarácsra is. Egy ilyen úgy keletkezik, hogy egy paralelogramma egyik csúcsából induló oldalegyeneseire mindkét irányban rámérjük az oldalt ismételten minden határon túl, majd a keletkező pontokon át a másik oldalegyenessel párhuzamos egyenest húzunk. A két egyenessereg metszéspontjai a keletkező paralelogrammarács rácspontjai.*
Jelöljük a kiválasztott paralelogrammacsúcsot O-val, a belőle induló oldalakat mint vektorokat a és b-vel, ekkor világos, hogy a rácspontok az ua+vb helyvektorú pontok, ahol u és v tetszés szerinti egész szám.
Legyen E, F, G három rácspont, helyvektoraik e, f, g. Ekkor G-nek az EF szakasz felezőpontjára vonatkozó G' tükörképére GG'→=GE→+GF→. Így G' helyvektorára
g'=g+GE→+GF→=g+(e-g) +(f-g)=e+f-g.  
Mivel a jobb oldalon álló vektorok mindegyike a és b egy-egy egész többszörösének az összege, így ugyanez áll g'-re is, tehát G' rácspont. Meggondolásunk akkor is helyes marad, ha E és F egybeesik, tehát rácspontnak rácspontra vonatkozó tükörképe is rácspont.
 

II. megoldás: A feladat állításának helyességét tetszés szerinti síkrácsra bizonyítjuk. Felhasználjuk ezeknek a következő tulajdonságát: Ha egy egyenesen van két rácspont, akkor van végtelen sok, ezek egymástól egyenlő távolságra sorakoznak; a sík összes rácspontjai ezzel párhuzamos egyeneseken helyezkednek el, mindegyiken egymástól ugyanolyan távolságra, és az egyenesek is egymástól egyenlő távolságra következnek. Ezt a megoldás végén bebizonyítjuk. A legalább két rácspontot tartalmazó egyeneseket rácsegyenesnek fogjuk nevezni.
Azt mutatjuk meg, hogy ha egy PQRS négyszög csúcsai rácspontok, és az EPQ háromszög P-n és Q-n kívül nem tartalmaz rácspontot sem a határán sem a belsejében, akkor
PQR∢+QPS∢≧180∘.
Ez egyenértékű a bizonyítandó állítással.
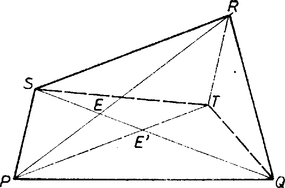
Feltétel szerint a PQ egyenesen és a vele párhuzamos rácsegyeneseken a szomszédos rácspontok távolsága a PQ szakasz hossza. Vegyük a PQ egyenesnek a négyszöget tartalmazó oldalán az első, PQ-val párhuzamos rácsegyenest és azon a QE egyeneshez legközelebbi A rácspontot a QE egyenes P-t tartalmazó oldalán, esetleg QE-n, továbbá a szomszédos B rácspontot úgy, hogy APQB paralelogramma legyen (8. ábra). Ekkor E az AP és BQ egyenesek közti sáv pontja, mert az A és B rácspont választása folytán az EPQ háromszög vagy benne van az APQB paralelogrammában, vagy az AB egyenes átmetszi a háromszöget. Utóbbi esetben az egyenesnek a háromszögbe eső szakasza az AB szakasz része, mert a háromszög nem tartalmaz rácspontot.
 
8. ábra

A sáv belsejében nincs rácspont, mert ha volna, az azon keresztülmenő, AP-vel párhuzamos rácsegyenesnek AP hosszúságú szakasza esnék az APQB paralelogrammába, és ennek vagy a két végpontja, vagy egy belső pontja rácspont volna; a paralelogramma azonban nem tartalmaz a csúcsain kívül rácspontot.
Eszerint R és S, amelyek a PE, ill. a QE meghosszabbítására esnek, a sávon kívül vannak, annak különböző oldalán, vagy a sáv egyik, ill. másik határán. Így
PQR∢+QPS∢≧PQB∢+QPA∢=180∘,
és ezt kellett bizonyítanunk.
A felhasznált segédtétel bizonyítása. Legyen K,L,M három rácspont, amelyek nincsenek egy egyenesen. Tegyük fel továbbá, hogy L a KL félegyenesnek a K-hoz legközelebbi rácspontja. Az előző megoldáshoz fűzött 2. megjegyzésbeli tétel szerint K-nak az LM szakasz F felezőpontjára vonatkozó M1 tükörképe rácspont (9. ábra). Ez az M-en át KL-lel párhuzamosan húzott egyenesen van, és M és M1 közt nincs rácspont, mert annak F-re vonatkozó tükörképe K és L közti rácspont volna, ilyen azonban nincs.
 
 
9. ábra
 

Hasonlóan M-nek LM1 felezőpontjára vonatkozó L1 tükörképe, majd L-nek L1M1 felezőpontjára vonatkozó M2 tükörképe és így tovább, mindig a következő rácspontot adja, felváltva a KL és az MM1 egyenesen. K és L szerepét felcserélve adódik, hogy az egyeneseken az ellenkező irányban is végtelen sok rácspont van, egymástól egyenlő távolságra.
Ezzel eddig annyit láttunk be, hogy a KL egyenesen végtelen sok rácspont sorakozik egymástól egyenlő távolságra; továbbá egy M rácsponton át KL-lel párhuzamosan húzott egyenes szintén rácsegyenes, és ezen a szomszédos rácspontok távolsága szintén a KL távolság.
A KLM1M paralelogrammában csak véges sok rácspont lehet, viszont a KL és MM1 közti sávban minden KL-lel párhuzamos rácsegyenesen van a paralelogrammához tartozó rácspont, amint a megoldás első részében beláttuk. Így a sávban csak véges számú ilyen rácsegyenes futhat. Feltehetjük, hogy MM1 már a legközelebbi, tehát a paralelogramma nem tartalmaz e csúcsain kívül rácspontot.
Húzzuk meg az LM1 rácsegyenes minden rácspontján át a KL-lel párhuzamos rácsegyenest. Ezek együtt tartalmazzák az összes rácspontot. Ha ugyanis valamelyik két szomszédos egyenes közt volna még rácspont, azt tartalmazná egy KLM1M-mel egybevágó és egyállású K'L'M1'M' paralelogramma (9. ábra, az egyező betűk megfelelő csúcsokat jelölnek). A két paralelogrammát a KM1' felezőpontjára való tükrözés egymásba viszi át, így a vesszős paralelogrammában levő további rácspontot a vesszőtlen paralelogramma egy rácspontjába. Ilyen azonban nincs, így egyenlő távolságban sorakozó egyenesekből álló rácsegyenesseregünk az összes rácspontot tartalmazza. Ezzel a segédtételt bebizonyítottuk.
 

III. megoldás. Felhasználjuk a paralelogrammarácsok következő tulajdonságát: Az olyan rácsháromszögeknek, amelyek sem belsejükben, sem a határukon nem tartalmaznak további rácspontot, egyenlő a területe. Az ilyen háromszögeket üresnek fogjuk nevezni.
A feladat állítását indirekt úton bizonyítjuk, tehát feltesszük, hogy az EPQ háromszög nem tartalmaz P-n és Q-n kívül rácspontot. Legyen az EPS háromszög PQ egyeneshez legközelebbi, P-től különböző rácspontja S1 (ez lehet S is, 10. ábra).
 
 
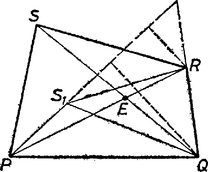10. ábra
 

Egyfelől a PRS1 háromszög területe kisebb a PQS1-énél, mert a szögfeltételből következik, hogy a PS1 és a QR egyenesek S1-en, ill. R-en túli meghosszabbítása metszi egymást. Így a PS1 oldalhoz tartozó magasság az előző háromszögben kisebb, mint az utóbbiban.
Másfelől nézve PQS1 üres rácsháromszög, mert ha tartalmazna rácspontot a csúcsain kívül, ez közelebb lenne PQ-hoz, mint S1, és az EPQ háromszögön kívül lenne az indirekt feltevés szerint, de ez S1 választása szerint nem lehetséges.
A PRS1 háromszög szintén rácsháromszög, és vagy üres, vagy felbontható több üres rácsháromszögre, területe tehát legalább akkora, mint a PQS1, háromszögé. Ezzel ellentmondásra jutottunk, tehát feltevésünk nem lehet igaz.
 

Megjegyzések: 1. Lényegében a felhasznált segédtétel volt az 1942. évi verseny 2. feladata. Több bizonyítás található rá az előzőkben idézett könyv 110‐117. oldalán.
2. Tetszés szerinti rácssokszög területe meghatározható rácspontjainak a megszámolásával. Az üres rácsháromszögek területét h-val jelölve, ha a sokszög belsejében b rácspont van, a kerületén a csúcsokat is beleszámítva, k darab, akkor a sokszög területe (2b+k-2)h. Ezt a G.Pick-től származó tételt* felhasználva elvégezhető a fenti bizonyítás az S1 pont segítségül vétele nélkül a PQS és a PRS háromszög területének összehasonlításával is.
*Több megoldás található rá lapunk II. Évf. 235‐240. oldalán.

*Lásd Matematikai Lapok XVI. (1965) 93. és 100‐101. old.

*Paralelogrammarácsok tulajdonságairól szól pl. Hajós Gy.‐Neukomm Gy.‐Surányi J.: Matematikai Versenytételek II., 3. kiadás, Tankönyvkiadó, Budapest, 1988. 111‐112. old. jegyzete.

*Az állítás könnyen következik az üres rácsháromszögekre vonatkozó tételből. Lásd az idézett könyv 117. oldalának jegyzetét. Szép közvetlen bizonyítást adott Pólya György és tőle függetlenül Somogyi árpád. Lásd G. L. Alexanderson és Jean Andersen: Pólya György élete és munkássága (ford.: Pataki Béláné), Matematikai Lapok 33 (1982‐1986) 225‐233. old.; lásd közelebbről a 229‐233. oldalt. (Megjegyzendő, hogy ott a 2(a), 2(b) ábrán a szaggatott vonalak feleslegesek, a folytonosak közül kellene minden másodiknak szaggatottnak lennie.)