Kezdőlap


Feladat:	1987. évi Kürschák matematikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Benczúr András , Dinnyés Enikő , Drasny Gábor , Fleiner Tamás , Gács András , Keleti Tamás , Lengyel Csaba , Lipták László , Rimányi Richárd , Tasnádi Tamás
Füzet:	1988/február, 52 - 56. oldal		PDF \| MathML
Témakör(ök):	Térgeometria alapjai, Ponthalmazok, Halmazok számossága, Koordináta-geometria, Függvények, Függvényegyenletek, Egész együtthatós polinomok, Valós együtthatós polinomok, Hengerek, Parabola, mint kúpszelet, Trigonometrikus függvények, Sík egyenlete, Trigonometriai azonosságok, Harmadfokú (és arra visszavezethető) egyenletek, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1988/február: 1987. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Van ilyen ponthalmaz és nagyon sokféleképpen lehet ilyent megadni. Egy derékszögű koordinátarendszerben a pont koordinátáit $x$ , $y$ , $z$ -vel jelölve minden sík egyenlete írható

\begin{matrix} a x + b y + c z + d = 0 \end{matrix}

alakban, ahol

a

b

c

közt van

0

-tól különböző. A ponthalmazt úgy adjuk meg, hogy minden valós

t

értékhez hozzárendeljük azt a pontot, amelyiknek koordinátái

\begin{matrix} x = f (t), y = g (t), z = h (t) . \end{matrix}

f

g

h

függvényeket úgy kell választanunk, hogy az

\begin{matrix} a f (t) + b g (t) + c h (t) + d = 0 \end{matrix}

egyenletnek legyen legalább egy gyöke, ha

a

b

c

közül legalább az egyik nem

0

, de mindig csak véges sok gyöke legyen.
Kézenfekvő polinomokat választani, mert tudjuk, hogy egy polinomnak csak véges sok gyöke lehet: legfeljebb annyi, mint a foka, kivéve természetesen a

0

polinomot. Azt is tudjuk továbbá, hogy (valós együtthatós) páratlan fokú polinomnak mindig van legalább egy (valós) gyöke. Ezek alapján az

x = t^{5}

y = t^{3}

z = t

összefüggésekkel jellemzett ponthalmaz megfelel. Ezt írhatjuk kicsit egyszerűbben

\begin{matrix} x = z^{5}, y = z^{3} \end{matrix}

alakban is. Valóban, az

\begin{matrix} a z^{5} + b z^{3} + c z + d = 0 \end{matrix}

egyenlet a mondott feltételek mellett mindig páratlan:

5

-öd-,

3

-ad- vagy elsőfokú, így a ponthalmaznak minden síkkal legalább egy és legfeljebb

5

közös pontja van.

Megjegyzések. 1. Mint a megoldás is utal rá,

f

g

h

-nak bármilyen három különböző, páratlan fokú polinomot választhatunk. Használhatunk páros fokú polinomot is alkalmas előjel-megállapodásokkal kombinálva. Könnyű látni pl., hogy a következő ponthalmaznak:

\begin{matrix} z = x^{3}, y = {\begin{matrix} x^{2}, ha x \geq 0, \\ - x^{2} ha x < 0 \end{matrix} \end{matrix}

szintén van pontja minden síkon és mindegyiken csak véges számú. Belátható, hogy ennek is legfeljebb

5

pontja lehet egy síkon. Ennek igazolását az olvasóra bízzuk.

2. A megadott ponthalmazok pontjai térbeli görbét alkotnak. Az előző megjegyzésben szereplő görbéhez eljuthatunk úgy, hogy az

x

- és

z

-tengely síkjában megrajzoljuk a

z = x^{3}

egyenletű görbét és tekintjük az ennek a pontjain át az

y

tengellyel párhuzamosan húzott egyenesek alkotta (általános) hengerfelületet; az

y

- és

x

-tengely síkjában pedig az origóban érintkező, első, ill. harmadik negyedben futó két félparabolaívből álló görbe pontjain át a

z

-tengellyel párhuzamosan húzott egyenesek alkotta hengerfelületet képezzük. A két felület metszésvonala adja a szóban forgó görbét (1. a, b, c ábra).

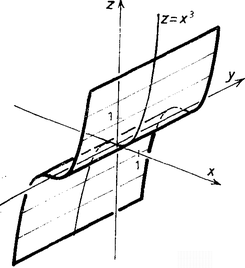1.a ábra

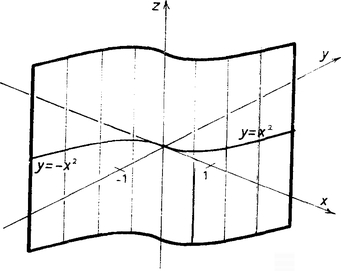1.b ábra

1.c ábra

3. Használhatók polinomok helyett más függvények is. Erre mutat példát a következő megoldás.

II. megoldás. Három térbeli görbe vonalat adunk meg, amelyek egyesítésére teljesülnek a követelmények. Ezek szemléletesen így származtathatók. Egy

2 π

szélességű végtelen sáv középvonala legyen az ordinátatengely. Ábrázoljuk a

tg\frac{φ}{2}

függvényt a

- π < φ < π

számközben (2.a ábra), majd hajlítsuk össze a sávot egy (egységnyi sugarú) hengerré. A henger három példányát helyezzük el úgy, hogy a tengelyük rendre az

x

y

z

-tengely legyen, a sáv (

0,0

) pontja pedig az

y

z

-, illetőleg

x

-tengely egységpontjába kerüljön. (A 2.b ábra a harmadik hengert ábrázolja.)

2.a ábra

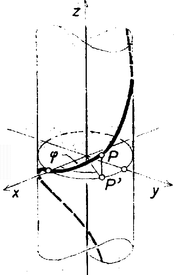2.b ábra

A feltételek teljesülésének igazolásához célszerű a pontok koordinátáit formulákkal megadni. A

z

-tengely körüli henger egy pontja legyen

P

, vetülete az

x

y

koordinátasíkon

P'

, az ehhez mutató vektornak az

x

-tengely pozitív felével bezárt szöge

φ

. Ekkor az (

1

0

0

) ponttól

P'

-ig terjedő körív hossza is

φ

, így a

P

pont koordinátái:

\begin{matrix} x = cos φ, y = sin φ, z = tg\frac{φ}{2}. \end{matrix}

A másik két görbe pontjainak koordinátái:

\begin{matrix} x = tg\frac{φ}{2},  y=cosφ,  z=sinφ,  ill.x=sinφ,  y= tg\frac{φ}{2},  z=cosφ; \end{matrix}

φ

mindhárom esetben

- π

és

π

közti szöget jelent (radiánban mérve).
Egy tetszés szerinti sík egyenlete

\begin{matrix} a x + b y + c z + d = 0 \end{matrix}

(1)

alakú, ahol

a

b

c

közt van

0

-tól különböző. Ennek a harmadik görbével való metszéspontjai azok a pontok, amelyek koordinátái az

\begin{matrix} a cos φ + b sin φ + c tg \frac{φ}{2} + d = 0 \end{matrix}

egyenletnek eleget tévő

φ

értékekhez az első egyenlethármassal meghatározott értékek.
Az egyenlet

t = tg\frac{φ}{2}

-re vonatkozó algebrai egyenletté alakítható a következő összefüggések felhasználásával:

\begin{matrix} sin φ = \frac{2 sin \frac{φ}{2} cos \frac{φ}{2}}{sin^{2} \frac{φ}{2} + cos^{2} \frac{φ}{2}} = \frac{2 t}{t^{2} + 1}; \\ cos φ = \frac{cos^{2} \frac{φ}{2} - sin^{2} \frac{φ}{2}}{sin^{2} \frac{φ}{2} + cos^{2} \frac{φ}{2}} = \frac{1 - t^{2}}{1 + t^{2}} . \end{matrix}

Ezeket beírva, a törteket eltávolítva és az egyenletet rendezve kapjuk, hogy:

\begin{matrix} c t^{3} + (d - a) t^{2} + 2 b t + a + d = 0. \end{matrix}

(2)

Ennek legfeljebb

3

megoldása van (a valós számok körében), kivéve, ha az azonosan

0

polinomról van szó, vagyis ha

\begin{matrix} b = c = d - a = a + d = 0. \end{matrix}

Ekkor azonban

a

és

d

0

, s így az (1) egyenlet minden (

x

y

z

) számhármasra teljesül, nem sík egyenlete. Mivel

tg\frac{φ}{2}

- π < φ < π

számközben minden valós értéket felvesz, és mindegyiket csak egyszer, így a síknak a görbével legfeljebb

3

közös pontja lehet.
Ugyanígy adódik, hogy egy síknak a másik két görbével is legfeljebb

3

3

közös pontja lehet, az egész ponthalmazzal tehát legfeljebb

9

.
Az is világos, hogy minden síknak van közös pontja a halmazzal, mert ha pl.

c \neq 0

, akkor a (2) egyenlet harmadfokú és így van valós gyöke.

Megjegyzések. 1. Szemléletesen a hengert elmetszettük egy síkkal, és azt kérdezzük, hogy ha a hengerfelületet egy alkotója mentén felvágjuk és a síkba terítjük, a metszésvonal hány pontban metszi a tangensgörbe képét. Belátjuk, hogy ha a sík metszi a henger tengelyét, de nem merőleges rá, akkor a metszésvonal a síkba terítve egy szinuszvonalat ad.
Valóban, a henger egy tetszés szerinti pontjának koordinátái

x = cos φ

y = sin φ

z

alakban írhatók, így az (1) síkkal való metszéspontokat azok a

φ

értékek szolgáltatják, amelyekre

\begin{matrix} a cos φ + b sin φ + c z + d = 0. \end{matrix}

A síkra kimondott feltételek akkor teljesülnek, ha

c

, továbbá

a

és

b

közül legalább az egyik nem

0

. Ekkor egyenletünk így alakítható át:

\begin{matrix} z = - \frac{a}{c} cos φ - \frac{b}{c} sin φ - \frac{d}{c} = \frac{\sqrt[]{a^{2} + b^{2}}}{c} sin (φ - α) - \frac{d}{c}, \end{matrix}

ahol

α

-t a

\begin{matrix} sin α = \frac{- a}{\sqrt[]{a^{2} + b^{2}}}, cos α = \frac{b}{\sqrt[]{a^{2} + b^{2}}} \end{matrix}

összefüggések határozzák meg. Ezzel a kimondott állítást igazoltuk. A fenti meggondolás azt a szemléleti megfigyelést igazolja, hogy a két vonalnak legfeljebb

3

metszéspontja lehet.

2. Megfelelő ponthalmazok számtalan más elgondolás alapján is elkészíthetők, és merült is fel sok további példa a dolgozatokban. Többen állították azonban azt is, egyesek indokolni is próbálták, hogy a kívánt tulajdonságú ponthalmaz nem létezik.

3. A felmerült példák mindegyikében volt olyan sík, amelyik a ponthalmaznak legalább

5

pontját tartalmazta. Kézenfekvő kérdés, hogy nem adható-e meg olyan ponthalmaz, amelyiknek minden síkon

5

-nél kevesebb pontja van. Nem csökkenthető ez a szám

3

alá, hiszen a halmaz bármely

3

pontján át fektethető sík. Mély halmazelméleti módszerekkel bebizonyítható, hogy létezik olyan ponthalmaz is, amelyiknek minden síkon pontosan

3

pontja van. Ez a bizonyítás azonban csupán a ponthalmaz létezését adja, előállításához vagy egyáltalán az elképzeléséhez sem ad semmilyen támpontot.
Megmutatható hogy egy folytonos vonalnak, ha kielégíti a feltételeket, mindig van

5

egy síkban lévő pontja.