Feladat: 1983. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Birkás György ,  Erdős László ,  Hetyei Gábor ,  Kós Géza ,  Magyar Ákos ,  Megyesi Gábor ,  Náray Miklós ,  Poór István ,  Szabó Csaba ,  Szabó Zoltán ,  Törőcsik Jenő 
Füzet: 1984/február, 56 - 60. oldal  PDF  |  MathML 
Témakör(ök): Sík geometriája, Háromszögek nevezetes tételei, Maradékos osztás, Geometriai egyenlőtlenségek, Kombinatorikai leszámolási problémák, Egyéb szinezési problémák, Kör geometriája, Szabályos sokszögek geometriája, Ponthalmazok, Halmazok számossága, Pont körüli forgatás, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1984/február: 1983. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A megoldáshoz a feltételt átfogalmazzuk. Megmutatjuk a következőt: Ha A, B és Q nem egy egyenesen levő pontok, akkor síkjuknak azokra és csak azokra a C pontjaira tartalmazza az ABC háromszög belsejében a Q pontot, amelyek az AQB konvex szög csúcsszög-tartományának belsejében vannak (1. ábra).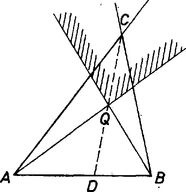

 
 
1. ábra
 

Valóban, ha Q a háromszög belsejében van, akkor C az AQ egyenesnek a B-t nem tartalmazó partján van, a BQ egyenesnek pedig az A-t nem tartalmazó partján. Így C a két félsík közös részében, tehát az állításban szereplő szögtartományban van. A konvex szögtartományról van szó, tehát arról, amelyik bármely két pontjával azok összekötő szakaszát is tartalmazza, miután a félsík konvex tartomány és konvex tartományok közös része is konvex.
Fordítva, ha C a mondott szögtartományban van, akkor a CQ egyenes Q-n túli meghosszabbítása metszi az AB szakaszt egy belső D pontjában. A CD szakasz az ABC háromszögben van, tehát annak Q belső pontja a háromszög belső pontja.
A feladatra térve a P1Q egyenes egyik, mondjuk jobb partján levő pontok számát (P1-et nem számítva) jelöljük r-rel, a bal parton levőket s-sel. A jelölést, ha kell, változtassuk meg úgy, hogy a jobb parton a P2,...,Pr+1 pontok legyenek, mégpedig úgy, hogy
P1QP2∢<P1QP3∢<...<P1QPr+1∢<180∘
teljesüljön.
A PiQ és Pi+1Q félegyenes Q-n túli félegyenesei közti szögtartományok a bal parton vannak és a különböző i-khez tartozóknak nincs közös pontjuk. Minden ilyen tartományban van legalább egy a bal parti pontok közül, mert a Pi, Pi+1-hez megfelelő Pk pontoknak segédtételünk szerint itt kell lenniük. A szögtartományok száma r, így
r≤s.
A bal és jobb part szerepét felcserélve ugyanígy azt nyerjük, hogy
s≤r.
Így az összes Pi pontok száma:
n=r+s+1=2r+1,
tehát páratlan szám, és ezt kellett bizonyítanunk.
 

Megjegyzések. 1. A versenyzők túlnyomó része a megoldásban szereplő lemmát sok más, általában nem ilyen ügyes módon használta fel.
a) Sokan egy egyenest forgattak a Q pont körül és annak két félegyenesét pirosra, ill. zöldre festettnek gondolva megállapították, hogy forgatás közben felváltva egyszer a piros, legközelebb a zöld félegyenes halad át egy-egy Pi ponton. 180∘-os elforgatás után ér vissza az egyenes először egy már érintett Pi ponthoz, de ezen most az egyenes másik félegyenese halad át, mint a kiindulásnál, ezért ezzel a másodszor érintett ponttal együtt összesen páros számú ponton halad át az egyenes, másrészt n+1-en, tehát n páratlan.
b) Mások azt vették észre, hogy a feladat feltételei nem változnak, ha a Pi pontokat a Q-ból induló, rajtuk átmenő félegyenesen elmozdítjuk, hiszen ha A és A1, B és B1, C és C1 egy-egy Q-ból induló félegyenesen van, akkor az ABC és A1B1C1 háromszöget nézve, vagy mindkettő belsejében tartalmazza Q-t, vagy egyik sem (2. ábra). Ennek alapján egy Q középpontú körre helyezték át a Pi pontokat. Ha a kör Pi-vel átellenes pontját Ri-vel jelöljük, akkor megállapították, hogy a kör mentén haladva felváltva következik egy P és egy R pont. A P pontok száma helyett az átmérőket számolták össze egy félkörre eső végpontjaik szerint. Ha a P1 ponttal kezdjük a megszámlálást, akkor egy P ponttal is fejezzük be, mert R1 az első pont, amit már nem számolunk. Ebből ismét következik n páratlan volta.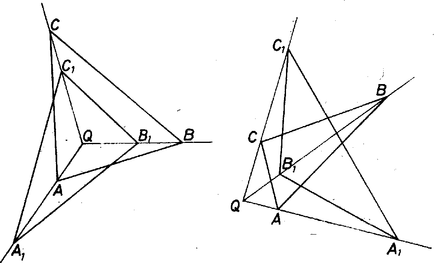
 
 
2. ábra
 

2. A versenyzők a segédtételt általában szemlélet alapján mondták ki. Ezt a bizottság nem tekintette hibának.
3. Többen megjegyezték, hogy a bizonyításban csak annyit használtunk ki, hogy egy Pi, egy Pj pont és Q nincs egy egyenesen, elég lett volna tehát ennyit feltételezni. Azt azonban már nem vették észre, hogy ezt meg nem kell külön feltenni, hiszen ha valamilyen i-re és j-re ez volna a helyzet, akkor semmilyen k-ra nem tartalmazhatná a PiPjPk háromszög belsejében a Q-t, tehát nem teljesülhetne a feladat másik feltétele.
4. Sokan megjegyezték, hogy minden páratlan n-re van a feltételeket kielégítő pontrendszer, pl. egy szabályos n-szög csúcsait választjuk Pi pontoknak és a középpontját Q-nak.
Többen felvetették azt a kérdést, hogy ha megadunk tetszés szerint páratlan számú pontot a síkban, van-e hozzájuk olyan Q pont, amivel teljesülnek a feladat feltételei. A közölt megoldás felhasználásával megmutatjuk, hogy a kérdésre tagadó a válasz.
A bizonyítás azt adta, hogy a P1Q egyenes egyik és másik partján ugyanannyi Pi pontnak kell lennie. Itt P1 helyett bármelyik Pi pontot vehettük volna. Azt bizonyítottuk tehát, hogy ha a feladat feltételei teljesülnek, akkor mindegyik PiQ egyenes egyik és másik partján ugyanannyi Pj pont van.
Ha most 3 nem egy egyenesen levő pont van adva, akkor az általuk meghatározott háromszög minden belső pontja választható Q-nak. Nem nehéz belátni azt sem, hogy ha 5 pont van a síkban, azokhoz is található megfelelő Q pont. Ha azonban 7 pontot pl. a 3. ábrán látható módon adunk meg, akkor nem található hozzájuk megfelelő 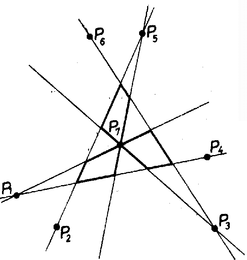Q pont.
 
 
3. ábra
 

Valóban, Q a feladat feltételeinek fent megfogalmazott következménye szerint olyan kell hogy legyen, hogy pl. a QP1 egyenes mindkét partján 3‐3 Pi pont legyen. Ez csak a P4P1P7 szögtartomány belsejében levő pontokra teljesül. Hasonlóan benne kell lennie Q-nak a P6P3P7 és a P2P5P7 szögtartomány belsejében is. A 3 szögtartománynak azonban egyetlen közös pontja P7, és az is határpontja mindegyiknek, tehát nincs megfelelő 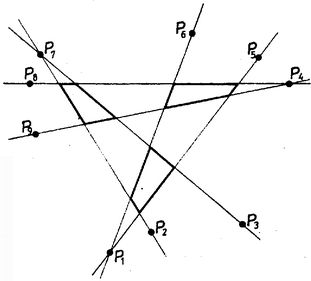Q pont.
 
 
4. ábra
 

A 4. ábra 9 pontja közt 3 olyan szögtartományt jelöltünk meg, amelyeknek még közös határpontjuk sincs, viszont ha volna alkalmas Q pont, annak mindegyik belsejében kellene lennie.
A következő megoldás a pontok megszámlálása helyett visszavezeti a problémát egy 2-vel kevesebb pontból álló rendszer esetére.
 

II. megoldás. Megmutatjuk, hogy ha egy P1,P2,...Pn, Q pontrendszerre teljesülnek a feladat feltételei, akkor minden Pa ponthoz található olyan Pb pont, hogy az e két pont elhagyása után visszamaradó pontrendszerre is teljesülnek. Ebből már következik, hogy n csak páratlan lehet, hiszen ha n>3, n pont közül pontpárok elhagyásával eljuthatunk páratlan számú pont esetén 3, páros számú n esetén 2 pontból álló rendszerhez, amelyre szintén teljesülnek a feladat feltételei. De 2 pont, P1 és P2 esetén nem teljesülhetnek, hiszen egyáltalán nem választható hozzájuk egy harmadik Ph pont, így semmilyen páros n-re sem teljesülhetnek a feltételek. n tehát csak páratlan lehet.
Teljesüljenek a P1,P2,...,Pn, Q pontokra a feladat feltételei. Kiválasztva tetszés szerint egy Pa pontot, forgassuk a PaQ egyenest Q körül valamelyik irányban, míg egy újabb Pb ponthoz nem ér. Nevezzük a Pi pontokból Pa és Pb elhagyásával visszamaradó pontrendszert D-nek. Mivel Pb volt az első pont, amibe a forgatott egyenes Pa elhagyása után beleütközött, a PaQ és PbQ egyenesek közti 4 szögtartomány közül egy csúcsszögeket alkotó párban nincs további Pi pont. Az I. megoldásban bizonyított segédtétel szerint a Pa, Pb-hez megfelelő Pk pontok a PaQ és PbQ szakaszok Q-n túli meghosszabbításai közti konvex szögtartomány belsejében vannak. Így ez és a PaQPb szögtartomány tartalmazza D-t.
Legyen P és Pj D-nek két pontja. Ha ugyanabban a szögtartományban vannak, akkor sem a PiPjPa, sem a PiPjPb háromszög nem tartalmazza Q-t (5. ábra), tehát a Pi, Pj-hez megfelelő Pk pontok D-hez tartoznak.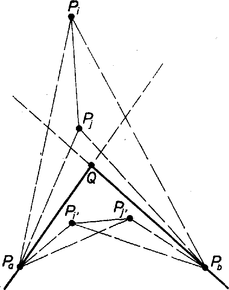
 
 
5. ábra
 

Ha Pi a PaQPb szögtartományban van, Pj a csúcsszög-tartományban, akkor feltehetjük, hogy a PiPj szakasz a QPa félegyenest metszi egy A pontban. Legyen Pk olyan pont, amelyre PiPaPk tartalmazza Q-t (6. ábr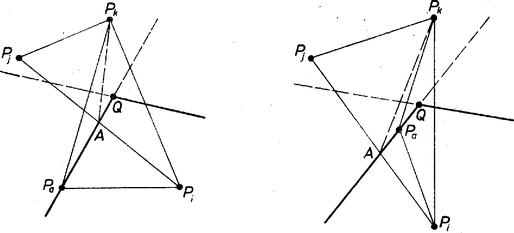a).
 
 
6. ábra
 


Mivel A a Q-ból induló QPa félegyenesen van, a PiAPk háromszög is tartalmazza Q-t. Az utóbbi háromszög része a PiPjPk háromszögnek, így ez is tartalmazza Q-t, tehát Pk a Pi, Pj pontpárhoz is megfelelő harmadik pont. Pk a D pontrendszer pontja, hiszen mint Pi és Pa-hoz megfelelő pont, az I. megoldás segédtétele szerint a PaQPi szögtartomány csúcsszög-tartományában van, és így a PaQPb szögtartományon kívül; Pk tehát különbözik Pa-tól és Pb-től. Ezzel beláttuk a megoldás elején megfogalmazott állítást és így a feladat állítását is.