Kezdőlap


Feladat:	1971. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bajmóczy Ervin , Berényi Péter , Füredi Zoltán , Komjáth Péter , Máté András , Móri Tamás , Ruzsa Imre
Füzet:	1972/február, 51 - 52. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Középpontos tükrözés, Síkgeometriai számítások trigonometriával, Vetítések, Magasságvonal, Középvonal, Eltolás, Vektorok, Vektorok lineáris kombinációi, Vektorok felbontása összetevőkre, Paralelogrammák, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1972/február: 1971. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a $B_{1}$ , $B_{2}$ , $C_{1}$ , $C_{2}$ pontok merőleges vetületét a háromszög $A$ -ból húzott magasságán $B'_{1}$ , $B'_{2}$ , $C'_{1}$ , $C'_{2}$ -vel. Az $A B$ és $A C$ oldal felezőpontjainak a vetülete a magasságon ugyanaz az $F'$ pont, miután a felezőpontokat összekötő egyenes, a háromszög középvonala, párhuzamos a $B C$ oldallal, tehát merőleges az $A$ -ból húzott magasságra (1. ábra). Így a $B'_{1} C'_{1}$ és a $B'_{2} C'_{2}$ szakaszok is egymás tükörképei, tehát egyenlő hosszúak (és ellenkező irányúak).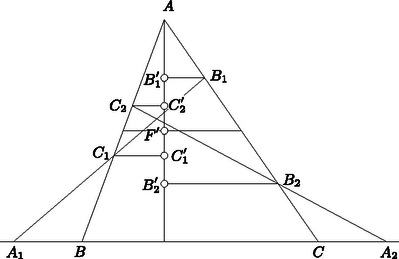

1. ábra

B'_{1} B_{1} C_{1} ∢

és a

B_{1} A_{1} C ∢

, továbbá a

C'_{2} C_{2} B_{2} ∢

és a

C_{2} A_{2} B ∢

szárai párhuzamosak, tehát sinusaik megegyeznek. Így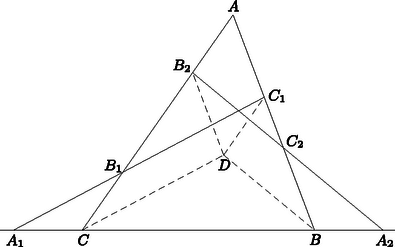

\begin{matrix} sin B_{1} A_{1} C ∢ = sin B'_{1} B_{1} C_{1} ∢ = \frac{B'_{1} C'_{1}}{B_{1} C_{1}}, \\ sin C_{2} A_{2} B ∢ = sin C'_{2} C_{2} B_{2} ∢ = \frac{C'_{2} B'_{2}}{B_{2} C_{2}} . \end{matrix}

A jobb oldali törtek számlálói egyenlők, így a bal és a jobb oldalak hányadosa is megegyezik, ami a kívánt egyenlőséget adja.

II. megoldás. Toljuk el a

B_{1} C_{1}

szakaszt a

B_{1} C

vektorral, legyen

C_{1}

új helyzete

D

(2. ábra). Ekkor

\begin{matrix} C_{1} D = B_{1} C, \end{matrix}

és a két szakasz egyirányban párhuzamos. A tükrözés folytán viszont az utóbbi szakasz

A B_{2}

-vel egyenlő és egyirányú. Így

A B_{2} D C_{1}

paralelogramma, tehát

B_{2} D

A C_{1}

és ‐ ismét a tükrözés folytán ‐

C_{2} B

egyirányú, egyenlő szakaszok. Ez viszont azt jelenti, hogy

B C_{2} B_{2} D

is paralelogramma,

D B

tehát

B_{2} C_{2}

-ből keletkezik párhuzamos eltolással.

2. ábra

A keletkezett

B C D

háromszögben

D C B ∢

és

D B C ∢

szárai párhuzamosak a

B_{1} A_{1} C ∢

, ill.

C_{2} A_{2} B ∢

száraival, s így sinusaik megegyeznek.
A

B C D

háromszögre a sinustételt alkalmazva nyerjük, hogy

\begin{matrix} \frac{B D}{C D} = \frac{B_{2} C_{2}}{B_{1} C_{1}} = \frac{sin D C B ∢}{sin D B C ∢} = \frac{sin B_{1} A_{1} C ∢}{sin C_{2} A_{2} B ∢} . \end{matrix}

Ezt kellett bizonyítanunk.

Megjegyzések. 1. Egyik bizonyításban sem használtuk ki azt, hogy

B_{1}

és

C_{1}

a megfelelő oldalszakaszon van. Így a feladat állítása igaz minden olyan egyenesre, amelyik metszi mind a három oldalegyenest és nem megy át

A

-n.
2. A feladat szövege kimondta ugyan, hogy a

B_{2} C_{2}

és

B C

egyenes metszi egymást, több versenyző rámutatott azonban, hogy ez következik már abból, hogy

B_{1} C_{1}

és

B C

metszik egymást. Valóban, az I. megoldásban az utóbbi tény azt jelenti, hogy

B'_{1}

és

C'_{1}

különböző, de ekkor

B'_{2}

és

C'_{2}

is, tehát

B_{2} C_{2}

sem párhuzamos

B C

-vel. A II. megoldásban a feltétel azt jelenti, hogy

D

nem esik

B C

-re. Ekkor azonban

D B

és a vele párhuzamos

B_{2} C_{2}

sem párhuzamos

B C

-vel.
3. Többen vektorszámítással oldották meg a feladatot, megmutatva hogy a

{\vec{B_{1} C}}_{1} + {\vec{B_{2} C}}_{2}

eredővektor párhuzamos (sőt egyenlő) a

\vec{C B}

vektorral. Ez könnyen adódik, ha pl. a fellépő vektorokat a

\vec{C A}

és

\vec{A B}

vektorokkal párhuzamos összetevőkre bontjuk.