| Feladat: | 1970. évi Kürschák matematikaverseny 1. feladata | Korcsoport: - | Nehézségi fok: nehéz |
| Megoldó(k): | Bajmóczy Ervin , Füredi Zoltán , Kóczy László , Martoni Viktor , Ruzsa Imre | ||
| Füzet: | 1971/május, 193 - 195. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Egyéb sokszögek geometriája, Geometriai egyenlőtlenségek, Oszthatóság, Egészrész, törtrész függvények, Alakzatok súlypontja (tömegközéppontja), Egyenlő szárú háromszögek geometriája, Maradékos osztás, Tengelyes tükrözés, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1971/február: 1970. évi Kürschák matematikaverseny 1. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Jelölje a sokszög hegyesszögeinek számát. Mivel minden hegyesszög kisebb, mint , a hegyesszögek összege kisebb, mint . A többi szögről csak annyit tudunk, hogy kisebbek, mint , így összegük kisebb, mint . Így az -szög szögösszege kisebb, mint Hozzátartozik még a feladathoz annak megmutatása, hogy ez a korlát el is érhető; más szóval, olyan -szöget kell konstruálnunk, melyben a hegyesszögek száma pontosan . Foglalkozzunk először azzal az esettel, amikor -mal osztható, vagyis . Ekkor . 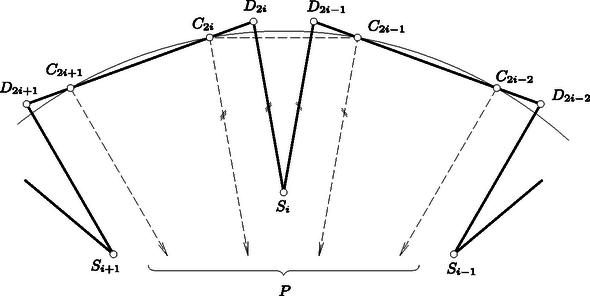 1. ábra Tekintsünk egy -os körcikket, legyen a körív két végpontja és , a körcikk csúcsa , és osszuk az ívet a , pontokkal egyenlő részre. Jelölje a háromszög súlypontját . Húzzunk -n át párhuzamost -gyel, és messe ez a egyenest -ben, -on -t értve. Hasonlóképpen legyen a -vel párhuzamos, -n áthaladó egyenesnek és -nek metszéspontja, -en -t értve (1. ábra). Tekintsük mármost a következő sokszöget: 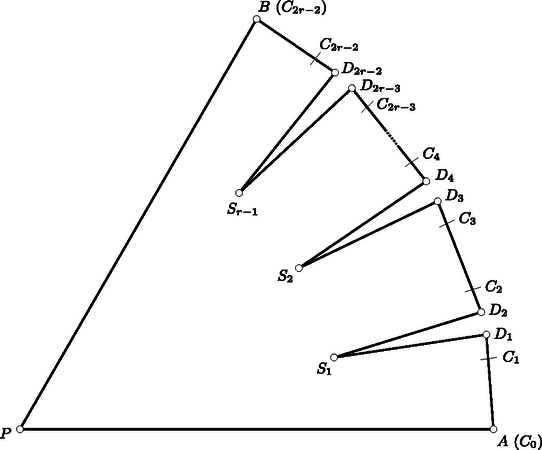 2. ábra Másodszor azzal az esettel foglalkozunk, amikor -mal osztva -et ad maradékul, vagyis . Ekkor . Az előzőek szerint tudunk olyan -szöget szerkeszteni, melynek hegyesszöge van. Tekintsük az előzőekben megszerkesztett sokszöget, és az oldal felező merőlegesén válasszunk egy olyan pontot, mely benne van a háromszögben. Ekkor és , tehát hegyesszögek, így a sokszög oldalát az töröttvonallal helyettesítve olyan -szöget kapunk, melyben hegyesszög van (3. ábra). 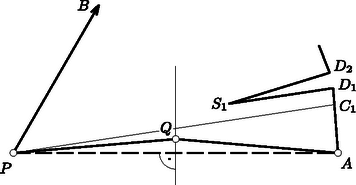 3. ábra Végül tekintsük az esetet. Tekintsük ismét a csúcsú sokszöget. Legyen , ill. -hez közelebbi) harmadolópontja , ill. , és -nek -re való tükörképe . Ekkor a sokszög , oldalait az töröttvonallal helyettesítve olyan sokszöget kapunk, melynek csúcsa és hegyesszöge van, hiszen a helyett fellépő három csúcs közül kettőben, -ben és -ben -os, vagyis hegyesszög van (4. ábra). 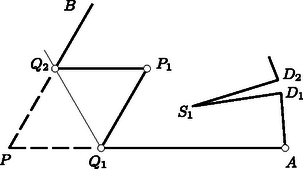 4. ábra 2. Számos más módon is konstruálható szögpontú, hegyesszöggel rendelkező sokszög. Több versenyző teljes indukcióval definiálta ezeket, -ről -ra lépve (ekkor , , esetére meg kell adni egy-egy példát, ami nyilvánvaló). A legtöbb megoldásban a fentihez hasonlóan volt megalkotva, de belőle -t és -t már igen sok különböző módon készítették el a versenyzők. 3. Több versenyző megjegyezte, hogy ha csak konvex sokszögekre szorítkoznánk, a hegyesszögek maximális száma volna. |