Kezdőlap


Feladat:	1966. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Babai László , Elekes György , Hoffmann György , Laczkovich Miklós , Lovász László , Pelikán József , Surányi László
Füzet:	1967/május, 193 - 196. oldal		PDF \| MathML
Témakör(ök):	Térgeometria alapjai, Négyzetek, Kör geometriája, Derékszögű háromszögek geometriája, Síkra vonatkozó tükrözés, Térbeli szimmetrikus alakzatok, Egyenlő szárú háromszögek geometriája, Vetítések, Pitagorasz-tétel alkalmazásai, Háromszög-egyenlőtlenség alkalmazásai, Geometriai egyenlőtlenségek, Középvonal, Szabályos tetraéder, Köréírt gömb, Kocka, Háromszög alapú hasábok, Szabályos sokszög alapú egyéb hasábok, Trapézok, Szimmetrikus sokszögek, Szabályos sokszögek geometriája, Négyszög alapú gúlák, Egyéb sokszögek egybevágósága, Permutációk, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1967/április: 1966. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A feladat követelményeit kielégítő $A B C D E$ ötszög keresésekor nyilván közömbös, hogy az oldalhosszat mekkorának választjuk. Kiindulhatunk ezért az egységoldalú $A B C O$ négyzetből, s azt vizsgáljuk, hogy a $D$ , $E$ csúcsok hol helyezkedhetnek el.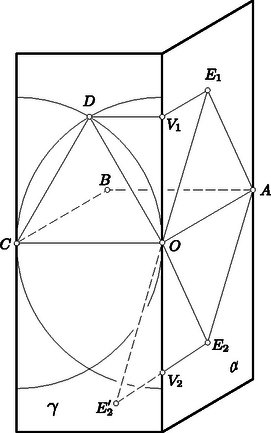
Minthogy $B C D ∢ = 90^{\circ}$ és $C D = 1$ , a $D$ pont abban a $γ$ síkban van, amely a $B C$ egyenest $C$ -ben merőlegesen metszi, mégpedig e sík $C$ középpontú, $C O$ sugarú körén helyezkedik el (1. ábra). A keresett ötszög átlói egyenlők, hiszen mindegyik egy-egy egységbefogójú egyenlőszárú derékszögű háromszög átfogója (közös hosszuk $\sqrt[]{2}$ ). Eszerint $A D = A C$ , s így a $D$ pont rajta van a $γ$ sík $O$ középpontú, $O C$ sugarú körén is, hiszen a $γ$ síkban ez a kör azoknak a pontoknak a mértani helye, amelyek $A$ -tól $A C$ távolságra vannak. A $D$ pont ezek szerint csak a mondott két kör valamelyik metszéspontja lehet. Az egyik metszéspontot önkényesen kijelölhetjük $D$ helyzetéül, hiszen a két metszéspont az $A B C$ síkra vonatkozólag szimmetrikusan helyezkedik el, s a keresett ötszöget is tükrözhetjük erre a síkra. $D$ helyzetéhez a legegyszerűbben úgy jutunk, hogy a $C O$ szakaszhoz a $γ$ síkban valamelyik oldalról egy szabályos háromszöget illesztünk, s ennek harmadik csúcsát tekintjük.

1. ábra

Ugyanígy okoskodhatunk az

E

pont helyzetét illetően is. Az adódik tehát, hogy ha a

B A

szakaszra

A

-ban merőlegesen emelt

α

síkban az

O A

szakaszhoz mindkét oldalról egy-egy szabályos háromszöget illesztünk, s ezek harmadik csúcsát

E_{1}

és

E_{2}

jelöli, akkor

E

csak ezek valamelyike lehet. Itt már mind a két lehetőségre gondolnunk kell, mert az

A B C

síkra vonatkozó tükrözés lehetősége

D

megválasztása után már nem áll fenn.
Bebizonyítjuk, hogy nincs kívánt tulajdonságú ötszög, mégpedig azért nincs, mert a

D E_{1}

és

D E_{2}

távolságok egyike sem egységnyi. Erről számítással könnyen meggyőződhetünk. Jelölje

V_{1}

E_{1}

pontnak a

γ

síkra vetett merőleges vetületét. A derékszögű

D V_{1} E_{1}

és

D E_{1} E_{2}

háromszögek befogóira

D V_{1} = V_{1} E_{1} = \frac{1}{2}

és

E_{1} E_{2} = \sqrt[]{3}

. Így tehát Pythagoras tétele szerint

\begin{matrix} D E_{1} = \sqrt[]{\frac{1}{4} + \frac{1}{4}} = \frac{1}{\sqrt[]{2}} < 1, \\ D E_{2} = \sqrt[]{\frac{1}{2} + 3} = \sqrt[]{\frac{7}{2}} > 1. \end{matrix}

A feladat kérdésére tehát valóban nemmel kell felelni.

Megjegyzések. Megoldásunkat többféleképpen is befejezhettük volna. Három ilyen lehetőséget említünk.
1. Az utolsó lépést kevesebb számolással is elintézhetjük. Evégett bevezetjük az

E_{2}

pont

γ

síkra vonatkozó

E'_{2}

tükörképét, amely egyben

E_{1}

tükörképe az

O

pontra vonatkozólag. A

D V_{1} E_{1}

és

D E'_{2} E_{1}

háromszögekre vonatkozó háromszög-egyenlőtlenségeket felhasználva

\begin{matrix} D E_{1} < D V_{1} + V_{1} E_{1} = \frac{1}{2} + \frac{1}{2} = 1, \\ D E_{2} = D E'_{2} > E'_{2} E_{1} - D E_{1} = 2 - D E_{1} > 1. \end{matrix}

A második becslésnél az első eredményét is felhasználtuk.
2. A

D E_{1} < 1

D E_{2} > 1

egyenlőtlenségek nyomban adódnak abból, hogy

D O E_{1} ∢ < 60^{\circ}

és

D O E_{2} ∢ > 60^{\circ}

. Elég az első helyességét belátnunk, hiszen

D O E_{2} ∢ = D O E'_{2} ∢

és ez a

D O E_{1} ∢

kiegészítő szöge, tehát az első egyenlőtlenség szerint

120^{\circ}

-nál is nagyobb. Az első egyenlőtlenség viszont a triéder oldalaira vonatkozó egyenlőtlenségből adódik, amely szerint

\begin{matrix} D O E_{1} ∢ < D O V_{1} ∢ + V_{1} O E_{1} ∢ = 30^{\circ} + 30^{\circ} = 60^{\circ} . \end{matrix}

3. Az adódott lehetőségek meg nem felelő volta abból is következik, hogy a

D E_{1}

és

D E_{2}

szakaszok egyike sem merőleges

C D

-re, vagyis abból, hogy az

E_{1}

E_{2}

pontok egyike sincs a

D C

-re

D

-ben merőlegesen emelt síkban. Ez a sík ugyanis merőleges

γ

-ra, tehát tartalmazza minden pontjának

γ

-ra vetett merőleges vetületét. Ez

E_{1}

és

E_{2}

esetében azt jelentené, hogy a

C D V_{1} ∢

és

C D V_{2} ∢

valamelyike derékszög (itt

V_{2}

E_{2}

pont vetületét jelöli), márpedig az első

120^{\circ}

, a második pedig

60^{\circ}

-nál kisebb, hiszen része a

C D O ∢

-nek.

II. megoldás. Azt állítjuk, hogy a követelményeket kielégítő ötszög átlóinak felezőpontjai egymástól mindannyian ugyanakkora távolságra vannak. Két ugyanabból a csúcsból kiinduló átló felezőpontjának távolsága az átlók által kifeszített háromszög középvonala, tehát a harmadik oldalnak, ötszögünk egy oldalának a fele. Egymáshoz nem csatlakozó átlók esetében első megoldásunknak arra a megállapítására támaszkodunk, hogy a

D

pont az

A B C O

négyzethez csatlakozó szabályos

C D O Δ

csúcsa. Az

A C

B D

átlók felezőpontjának távolságát keressük. Minthogy az

A C

B O

szakaszok felezőpontja azonos, a

B O

B D

szakaszok felezőpontjának távolságát kell meghatároznunk. Ez azonban a

B O D Δ

középvonala, s így az

O D

távolság fele, tehát szintén ötszögünk oldalának felével egyenlő.
Ezek szerint, ha van a feladat követelményeit kielégítő ötszög, akkor van a térben öt olyan pont, amelyek páronként egymástól ugyanakkora távolságra vannak. Minthogy azonban nincs öt ilyen pont, a feladat követelményeit kielégítő ötszög sincs.
Egymástól páronként ugyanakkora távolságra levő öt pont valóban nem létezik, mert közülük négy egy szabályos tetraédert határoz meg, s az ötödik, a tetraéder valamennyi csúcsától egyenlő távolságra elhelyezkedő pont csak a tetraéder köré írt gömb középpontja lehetne, de ennek a gömbnek a sugara a tetraéder élénél kisebb. (Ez a megoldás Kárteszi Ferenctől való.)

Megjegyzések. Első megoldásunk többféle befejezési lehetősége azt sejtetheti, hogy a feladat követelményeinek megfelelő lazítása után is nemmel kell a feladat kérdésére válaszolni. Megvizsgáljuk ezért, hogy különféle lazítások esetén mi a válasz.
1. Ha csak azt követeljük meg, hogy a térbeli ötszög oldalai közül négy legyen egyenlő, viszont minden szöge derékszög legyen, akkor már található a követelményt kielégítő ötszög. Ezt a 2. ábra példája mutatja, ahol az ötszög csúcsai egy kocka csúcsai közül valók.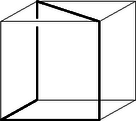

2. ábra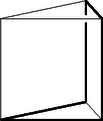

3. ábra

Ugyanígy található ötszög, ha az oldalak egyenlőségén kívül csak azt követeljük meg, hogy a szögek közül négy derékszög legyen. Ezt a 3. ábra mutatja, amely egy csupa egyenlő éllel rendelkező, szabályos háromoldalú hasáb éleiből alkotott ötszöget mutat be.
2. Igennel kell a feladat kérdésére válaszolni akkor is, ha a követelményeken mit sem enyhítünk, viszont öt helyett többoldalú sokszöget keresünk. Hat és nyolcoldalút könnyen alkothatunk egy kocka éleiből. Hétoldalúhoz jutunk, ha olyan szimmetrikus trapézből indulunk ki, amelynek szárai és egyik alapja egységnyiek, másik alapjának hossza pedig

\sqrt[]{2}

, majd ehhez egy egyenlőszárú derékszögű háromszöget, az egységnyi hosszúságú alaphoz pedig egy négyzetet illesztünk. Ha ezt a négyzetet a trapéz síkjára merőlegesen felhajtjuk, az egyenlőszárú derékszögű háromszöget pedig annyira hajtjuk fel, hogy befogói a trapézszárakra merőlegesek legyenek, akkor kívánt tulajdonságú hétszöghöz jutottunk el. Nyolcnál nagyobb oldalszámú ilyen sokszöget már könnyen találhatunk.
3. Ha olyan ötszöget keresünk, amelynek oldalai egyenlők, és bármely két szomszédos oldala ugyanakkora szöget alkot, nem követelve meg, hogy ez a szög derékszög legyen, akkor már nem felelhetünk a feladat kérdésére egyszerűen igennel vagy nemmel. Következő megoldásunk erre a kérdésre is válaszol.

III. megoldás. Felhasználjuk azt, hogy ha az

A

B

C

D

E

pontok távolságai rendre egyenlők az

A_{1}

B_{1}

C_{1}

D_{1}

E_{1}

pontok megfelelő távolságaival, akkor van olyan egybevágóság, amely az első pontötöst a másodikba viszi át. Ez öt helyett akárhány pontra is igaz, de mi csak öt pontra alkalmazzuk.
Azt vizsgáljuk, hogy melyek azok az ötszögek, amelyeknek oldalai egyenlők, és bármely két szomszédos oldaluk ugyanakkora szöget alkot. Bebizonyítjuk, hogy csak a síkbeli szabályos ötszög és az ennek átlóiból alakított szabályos csillagötszög ilyen, ahol is az egyenlő szögek nagysága

108^{\circ}

, illetve

36^{\circ}

. Bebizonyítjuk tehát azt is, hogy a feladat eredeti kérdésére nemmel kell válaszolni.
A bizonyításhoz abból indulunk ki, hogy az egyenlőoldalú és egyenlőszögű

A B C D E

ötszög átlói egyenlők, hiszen mindegyik egy-egy olyan egyenlőszárú háromszög alapja, amelynek szára és szárszöge az ötszög oldala és szöge. Az előrebocsátottak szerint van tehát olyan egybevágóság, amely az

A B C D E

ötszöget a

B C D E A

ötszögre helyezi, s ugyanezt az öt csúcs minden ciklikus permutációjáról is elmondhatjuk. Ezek az egybevágóságok az öt pont konvex burkát is önmagára helyezik, s mivel van közöttük olyan, amely csúcsa a konvex buroknak, a ciklikus permutáció szabad megválaszthatósága miatt mind az öt pont ilyen.
Ha az öt pont nincs egy síkban, akkor a konvex burkuk ötcsúcsú poliéder, tehát csak négyoldalú gúla vagy háromoldalú kettősgúla (két közös lapú tetraéder egyesítése) lehet. Mindkettőnek van háromélű csúcsa és négyélű csúcsa is. Minthogy azonban háromélű csúcsot egybevágóság nem vihet át négyélű csúcsba, ellentmondásra jutottunk. Ha tehát az ötszög nem síkbeli, akkor nem lehet minden oldala és minden szöge egyenlő.
Ha az öt pont egy síkban van, akkor konvex burkuk a fentiek szerint olyan ötszög, amelynek csúcsai egybevágósággal szabadon permutálhatók. Az öt pont konvex burka ezért csak szabályos ötszög lehet, s a keresett egyenlőoldalú és egyenlőszögű ötszöget vagy a szabályos ötszög oldalai, vagy annak átlói alkotják.