Kezdőlap


Feladat:	Gy.3116	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Babos Attila , Baharev Ali , Barát Anna , Biró Márton , Bodon Zsófia , Bujdosó Attila , Csendes Viktor , Csirmaz Előd , Csiszár Gábor , Davidovics Gábor , Farkas Milán , Fehér Lajos Károly , Führer Lívia , Gaál Zoltán , Gueth Krisztián , Gyenes Zoltán , Győri Nikolett , Hangya Balázs , Harangi Viktor , Hegedűs Péter , Hegyi Péter , Horváth Gábor , Kapinya Judit , Keszegh Balázs , Máthé András , Mecz Balázs , Nagy Kálmán , Naszódi Gergely , Papp Dávid , Pszota Anikó , Somodi Katalin , Szabó Péter , Székelyhidi Gábor , Szép László , Terpai Tamás , Vaik István , Végh László , Zábrádi Gergely
Füzet:	1997/december, 529 - 531. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Pitagorasz-tétel alkalmazásai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/február: Gy.3116

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy háromszögben a legnagyobb oldalhoz tartozik a legkisebb magasság. Mivel minden $a$ valós szám esetén igaz, hogy $4 a^{2} + 3 > a^{2} + a + 1$ és $4 a^{2} + 3 > a^{2} - a + 1$ , azért a feladatban szereplő háromszög legnagyobb oldala $\sqrt[]{4 a^{2} + 3}$ . Megmutatjuk, hogy az ehhez tartozó magasság, amit jelöljünk $k$ -val, legfeljebb 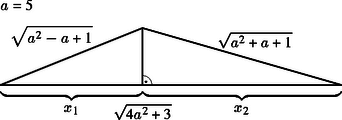$\frac{1}{2}$ .

Egy háromszög leghosszabb oldalán lévő szögek mindig hegyesszögek, ezért a leghosszabb oldalhoz tartozó magasság talppontja mindig az oldal belső pontja. Legyen

x_{1}

és

x_{2}

az a két szakasz, amelyre a talppont osztja ezt az oldalt. Ekkor

\begin{matrix} x_{1} + x_{2} = \sqrt[]{4 a^{2} + 3}, \end{matrix}

továbbá a keletkező két derékszögű háromszögben Pitagorasz tétele szerint

\begin{matrix} \begin{matrix} x_{1}^{2} + k^{2} & = a^{2} - a + 1, \\ x_{2}^{2} + k^{2} & = a^{2} + a + 1. \end{matrix} \end{matrix}

Ezekből kapjuk, hogy

\begin{matrix} 2 k^{2} = 2 a^{2} + 2 - (x_{1}^{2} + x_{2}^{2}) . \end{matrix}

\begin{matrix} \begin{matrix} x_{1}^{2} + x_{2}^{2} = \frac{1}{2} ({(x_{1} + x_{2})}^{2} + {(x_{1} - x_{2})}^{2}) = \frac{1}{2} ({(\sqrt[]{4 a^{2} + 3})}^{2} + {(\frac{x_{2}^{2} - x_{1}^{2}}{x_{1} + x_{2}})}^{2}) = \\ = \frac{1}{2} (4 a^{2} + 3 + {(\frac{2 a}{\sqrt[]{4 a^{2} + 3}})}^{2}) = \frac{1}{2} (4 a^{2} + 3 + \frac{4 a^{2}}{4 a^{2} + 3}), \end{matrix} \end{matrix}

ezért

\begin{matrix} 2 k^{2} = 2 a^{2} + 2 - (2 a^{2} + \frac{3}{2} + \frac{2 a^{2}}{4 a^{2} + 3}) = \frac{1}{2} - \frac{2 a^{2}}{4 a^{2} + 3} \leq \frac{1}{2} . \end{matrix}

Ebből pedig következik a bizonyítandó

k \leq \frac{1}{2}

egyenlőtlenség. Az is látszik, hogy egyenlőség pontosan akkor van, ha

a = 0

; ekkor a háromszög oldalai 1, 1 és

\sqrt[]{3}

Terpai Tamás, Fazekas M. Főv. Gyak. Gimn., II. o.t.) dolgozata alapján

Megjegyzés. Egyszerű számolással belátható, hogy minden valós

a

esetén

\sqrt[]{a^{2} - a + 1} + \sqrt[]{a^{2} + a + 1} > \sqrt[]{4 a^{2} + 3}

, azaz a két rövidebb oldal összhossza nagyobb, mint a harmadik oldal, tehát mindig létezik a feladatban szereplő háromszög.