Kezdőlap


Feladat:	Gy.3115	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barát Anna , Bérczi Gergely , Hangya Balázs , Lippner Gábor , Oláh Szabolcs , Terék Zsolt
Füzet:	1997/október, 413 - 414. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Magasságpont, Súlyvonal, Súlypont, Helyvektorok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/február: Gy.3115

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először megmutatjuk, hogy az $A B M$ , $B C M$ és $C A M$ háromszögek magasságpontjai rendre $C$ , $A$ és $B$ . Az $A B M$ háromszög $A$ -hoz tartozó magasságegyenese $A C$ , mert $A C ⊥ B M$ ; $B$ -hez tartozó magasságegyenese pedig $B C$ , mert $B C ⊥ A M$ . Ezért a háromszög magasságpontja $A C \cap B C = C$ . Ugyanígy látható be a $B C M$ és a $C A M$ háromszögre vonatkozó állítás is.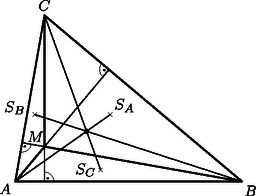

Jelöljük az

A B M

B C M

és

C A M

háromszögek súlypontjait rendre

S_{C}

S_{A}

és

S_{B}

-vel. Az előzőek alapján azt kell megmutatnunk, hogy a

C S_{C}

A S_{A}

és

B S_{B}

egyenesek egy ponton mennek át. Vektorok segítségével azt látjuk be, hogy e három szakasznak a rajtuk lévő súlyponthoz legközelebbi negyedelőpontjai egybeesnek. Legyenek az

M

-ből az

A B C

háromszög csúcsaihoz vezető vektorok

a

b

és

c

. Egy háromszög súlypontjának helyvektora megegyezik a csúcsok helyvektorai összegének harmadával, ezért

\begin{matrix} 3 \bar{M S_{C}} = a + b, 3 \bar{M S_{A}} = b + c és 3 \bar{M S_{B}} = c + a \end{matrix}

(hiszen az

M

pont helyvektora

0

). Egy szakasz egyik végpontjához legközelebbi negyedelőpontjának helyvektora pedig egynegyede a közelebbi végpont helyvektora háromszorosának és a távolabbi végpont helyvektora összegének. Így a

C S_{S}

A S_{A}

és

B S_{B}

szakaszok súlyponthoz legközelebbi negyedelőpontjainak helyvektorai:

\begin{matrix} \frac{1}{4} (3 \bar{M S_{C}} + c) = \frac{1}{4} (a + b + c) = \frac{1}{4} (3 \bar{M S_{A}} + a) = \frac{1}{4} (3 \bar{M S_{B}} + b) . \end{matrix}

Ez azt jelenti, hogy a három szakasz egy ponton megy át.

Megjegyzés. Bizonyításunk tetszőleges háromszögre helyes.