Feladat:	F.3176	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barta Ágnes ,  Blaskó Ádám ,  Czirok Levente ,  Dedinszky Zsófia ,  Forrai Gábor ,  Gyenes Zoltán ,  Hangya Balázs ,  Héjjas Péter ,  Jáger Márta ,  Juhász András ,  Lippner Gábor ,  Méder Áron ,  Nagy István ,  Pál András ,  Pintér Dömötör ,  Prohászka Benedek ,  Szalai-Dobos András ,  Szilágyi Judit ,  Szita István ,  Terék Zsolt ,  Terpai Tamás ,  Vaik Zsuzsanna ,  Várkonyi Péter
Füzet:	1997/december, 547 - 548. oldal		PDF  |  MathML
Témakör(ök):	Egyenes körhengerek, Köréírt gömb, Terület, felszín, Térfogat, Pitagorasz-tétel alkalmazásai, Harmonikus közép, Kvadratikus közép, Függvényvizsgálat differenciálszámítással, Szélsőérték-feladatok, Feladat
Hivatkozás(ok):	Feladatok: 1997/április: F.3176

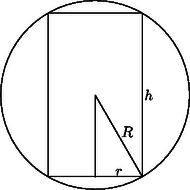
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen a gömb sugara $R$, a henger alapkörének sugara $r$, a henger magassága $h$. Mivel a henger és a gömb középpontja egybeesik, a Pitagorasz-tétel alapján $h=2\sqrt[]{R^2-r^2}$, a felszín és a térfogat hányadosa pedig $\begin{array}{c}{\displaystyle \frac{A}{V}=\frac{2\pi r\left(h+r\right)}{\pi r^{2}h}=\frac{2}{r}+\frac{2}{h}+\frac{2}{r}=\frac{1}{\sqrt[]{R^2-r^2}}\mathrm{.}}\end{array}$     Alkalmazzuk a súlyozott harmonikus és négyzetes közepek közötti egyenlőtlenséget az $\frac{r}{\sqrt[3]{2}}$ és $\sqrt[]{R^2-r^2}$ számokra a $\sqrt[3]{4}$ és 1 súlyokkal: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \left(\sqrt[3]{4}+1\right)\frac{V}{A}=\frac{\sqrt[3]{4}+1}{\sqrt[3]{4}\cdot \frac{\sqrt[3]{2}}{r}+\frac{1}{\sqrt[]{R^2-r^2}}}\le \sqrt[]{\frac{\sqrt[4]{4}\cdot {\left(\frac{r}{\sqrt[3]{2}}\right)}^2+{\sqrt[]{R^2-r^2}}^2}{\sqrt[3]{4}+1}}=\frac{R}{\sqrt[]{\sqrt[3]{4}+1}}\mathrm{,}}\end{array}}}\end{array}$ átrendezve $\begin{array}{c}{\displaystyle \frac{A}{V}\ge \frac{{\left(\sqrt[3]{4}+1\right)}^{\frac{3}{2}}}{R}\mathrm{.}}\end{array}$ A felszín és a térfogat hányadosát sikerült alulról becsülnünk egy, csak a gömb sugarától függő mennyiséggel. Egyenlőség akkor áll fenn, ha ugyanannak a két számnak vettük a közepeit, azaz $\frac{r}{\sqrt[3]{2}}=\sqrt[]{R^2-r^2}$. Ebből $r$-et kifejezve $\begin{array}{c}{\displaystyle r=\frac{\sqrt[3]{2}}{\sqrt[]{\sqrt[3]{4}+1}}R\text{és}h=2\sqrt[]{R^2-r^2}=\frac{2}{\sqrt[]{\sqrt[3]{4}+1}}R\mathrm{.}}\end{array}$ Ebben az esetben lesz a felszín és a térfogat hányadosa minimális, azaz $\frac{{\left(\sqrt[3]{4}+1\right)}^{\frac{3}{2}}}{R}$.   II. megoldás. Legyen $f\left(x\right)=\frac{2}{x}+\frac{1}{\sqrt[]{R^2-x^2}}$. Az előző megoldás szerint ennek a függvénynek a minimumát keressük a $\left(0;R\right)$ intervallumban. Ezt a derivált előjelének vizsgálatával végezzük. $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=-\frac{2}{x^2}+\frac{x}{{\left(R^2-x^2\right)}^{\frac{3}{2}}}=\frac{x^3-2{\left(R^2-x^2\right)}^{3/2}}{x^2{\left(R^2-x^2\right)}^{3/2}}\mathrm{.}}\end{array}$ A vizsgált intervallumban az utolsó tört nevezője mindig pozitív, a számlálója szigorúan monoton nő. Értéke akkor 0, amikor $x^3-2{\left(R^2-x^2\right)}^{3/2}=0$, azaz $x=\frac{\sqrt[3]{2}}{\sqrt[]{\sqrt[3]{4}+1}}R$. A $\left(0;\frac{\sqrt[3]{2}}{\sqrt[]{\sqrt[3]{4}+1}}R\right)$ intervallumban $f\text{'}<0$, és a függvény szigorúan monoton fogy, a $\left(\frac{\sqrt[3]{2}}{\sqrt[]{\sqrt[3]{4}+1}}R;R\right)$ intervallumban pedig $f\text{'}>0$, és $f$ szigorúan monoton nő. A függvény minimuma ezért az $x=\frac{\sqrt[3]{2}}{\sqrt[]{\sqrt[3]{4}+1}}R$ pontban van.   Megjegyzés. A feladatot deriválással megoldók között típushiba volt, hogy csupán a derivált nullhelyét keresték meg, de egyáltalán nem, vagy rosszul indokolták meg, hogy ott miért minimum van. Az sem teljes megoldás, ha valaki a második derivált előjele alapján csak annyit állapított meg, hogy az adott helyen a függvénynek lokális minimuma van.