Kezdőlap


Feladat:	Gy.3035	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bárány Kristóf , Barát Anna , Bérczi Gergely , Bosznay Tamás , Braun Gábor , Dedinszky Zsófia , Gyenes Zoltán , Horváth Gábor , Lippner Gábor , Nagy Endre , Naszódi Gergely , Páles Csaba , Sipos András , Szabó Gábor , Szandrocha Kamilla , Szepesi Zoltán , Terék Zsolt , Tótin Ágnes , Vaik Zsuzsanna , Végh László , Zubcsek Péter Pál
Füzet:	1996/október, 413 - 414. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Beírt kör, Terület, felszín, Háromszög-egyenlőtlenség alkalmazásai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1996/január: Gy.3035

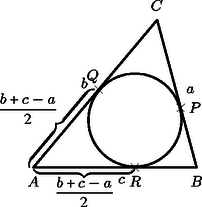
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög oldalait a szokásos módon $a$ , $b$ , $c$ -vel. Tudjuk, hogy egy külső pontból a körhöz húzott két érintőszakasz egyenlő hosszúságú. Ezért $A R = A Q$ , $B R = B P$ és $C P = C Q$ (ld. az ábrát). Tudjuk továbbá, hogy

\begin{matrix} \begin{matrix} A R + B R = c, \\ B P + C P = a, \\ C Q + A Q = b . \end{matrix} \end{matrix}

Ezt az egyenletrendszert megoldva kapjuk, hogy

\begin{matrix} \begin{matrix} A R = A Q = \frac{b + c - a}{2}, \\ B R = B P = \frac{a - b + c}{2} \\ C P = C Q = \frac{a + b - c}{2} . & és \end{matrix} \end{matrix}

Ismert, hogy ha két háromszögnek közös az egyik szöge, akkor területeik aránya megegyezik a közös szöget közrefogó oldalaik szorzatának arányával. Ezért

\begin{matrix} \frac{t_{A R Q}}{t_{A B C}} = \frac{{(\frac{b + c - a}{2})}^{2}}{b c}, \end{matrix}

vagyis

\begin{matrix} t_{A R Q} = \frac{{(b + c - a)}^{2}}{4 b c} \cdot t_{A B C} . \end{matrix}

Ugyanígy kapjuk, hogy

\begin{matrix} t_{B P R} = \frac{{(c + a - b)}^{2}}{4 a c} \cdot t_{A B C} és t_{C Q P} = \frac{{(a + b - c)}^{2}}{4 a c} \cdot t_{A B C} \end{matrix}

A bizonyítandó állítás ekvivalens azzal, hogy

\begin{matrix} t_{A R Q} + t_{B P R} + t_{C Q P} \geq \frac{3}{4} \cdot t_{A B C} . \end{matrix}

Ezt a fenti összefüggéseket felhasználva

\begin{matrix} \frac{{(b + c - a)}^{2}}{b c} + \frac{{(a - b + c)}^{2}}{a c} + \frac{{(a + b - c)}^{2}}{a b} \geq 3 \end{matrix}

(1)

alakban is írhatjuk. Az egyenlőtlenséget

2 a b c

-vel szorozva, majd rendezve kapjuk, hogy:

\begin{matrix} 2 a^{3} + 2 b^{3} + 2 c^{3} - 2 a^{2} b - 2 a b^{2} - 2 b^{2} c - 2 b c^{2} - 2 c^{2} a - 2 c a^{2} + 6 a b c \geq 0, \end{matrix}

azaz:

\begin{matrix} (b + c - a) {(b - c)}^{2} + (a - b + c) {(a - c)}^{2} + (a + b - c) {(a - b)}^{2} \geq 0. \end{matrix}

Ez viszont a háromszög-egyenlőtlenség miatt nyilvánvalóan teljesül. Mivel ekvivalens átalakításokat végeztünk, ezért (1) is teljesül. Ezzel beláttuk, hogy

t_{P Q R} \leq \frac{1}{4} t_{A B C}

Megjegyzés. Megoldásunkból az is látszik, hogy a

P Q R

háromszög területe pontosan akkor lesz az

A B C

háromszög területének egynegyede, ha a háromszög szabályos.