Kezdőlap


Feladat:	C.424	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Jáger Márta
Füzet:	1996/október, 404 - 405. oldal		PDF \| MathML
Témakör(ök):	Egyenes körkúpok, Térfogat, Pitagorasz-tétel alkalmazásai, Negyedfokú (és arra visszavezethető) egyenlőtlenségek, C gyakorlat
Hivatkozás(ok):	Feladatok: 1996/február: C.424

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a kör sugara $R = 1$ , egy körcikkhez tartozó középponti szög $\frac{360^{\circ}}{n}$ , az ívhossz $i = \frac{2 π}{n}$ .
A kúp alapkörének sugara $r$ . A $2 r π = \frac{2 π}{n}$ egyenletből

\begin{matrix} r = \frac{1}{n} . \end{matrix}

A kúp magasságát a Pitagorasz-tétellel számíthatjuk ki:

\begin{matrix} m = \sqrt[]{1 - {(\frac{1}{n})}^{2}} = \frac{1}{n} \sqrt[]{n^{2} - 1} . \end{matrix}

A kúpok együttes térfogata:

\begin{matrix} V = \frac{n {(\frac{1}{n})}^{2} π \frac{1}{n} \sqrt[]{n^{2} - 1}}{3} = \frac{π}{3} \frac{\sqrt[]{n^{2} - 1}}{n^{2}} . \end{matrix}

Kérdés, mikor lesz ez az összeg maximális.
A

\frac{\sqrt[]{n^{2} - 1}}{n^{2}} = \frac{1}{n} \sqrt[]{1 - \frac{1}{n^{2}}}

kifejezés ,,láthatóan'' csökken, ha

n

növekszik (és

n \geq 2

, hiszen legalább két körcikkre szétvágtuk a papírlapot):

\begin{matrix} n & 2 & 3 & 4 & 5 \\ \frac{\sqrt[]{n^{2} - 1}}{n^{2}} & 0,433 ... & 0,314 ... & 0,242 ... & 0,196 ... \end{matrix}

y = \frac{\sqrt[]{x^{2} - 1}}{x^{2}}

függvény számítógéppel készült grafikonját mutatja a 3. ábra.
Várható tehát, hogy a maximumot

n = 2

esetén kapjuk. Ehhez azt kell belátni, hogy

\begin{matrix} \frac{\sqrt[]{3}}{4} = \frac{\sqrt[]{2^{2} - 1}}{2^{2}} > \frac{\sqrt[]{n^{2} - 1}}{n^{2}}, han > 2 . \end{matrix}

Négyzetre emelve (

n^{2} - 1 > 0

), és rendezve

\begin{matrix} 3 n^{4} - 16 n^{3} - 16 > 0. \end{matrix}

n^{2}

-ben egy másodfokú kifejezés, alakítsuk teljes négyzetté:

\begin{matrix} 9 n^{4} - 48 n^{2} - 48 = {(3 n^{2} - 8)}^{2} - 16 > 0, \end{matrix}

ahonnan

{(3 n^{2} - 8)}^{2} > 16

, márpedig ha

n > 2

, akkor

3 n^{2} > 8

, és

\begin{matrix} {(3 n^{2} - 8)}^{2} > {(3 \cdot 2^{2} - 8)}^{2} = 4^{2} = 16. \end{matrix}

Ezzel állításunkat igazoltuk. A térfogatösszeg akkor maximális, ha a kört 2 körcikkre osztottuk.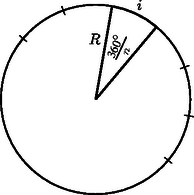