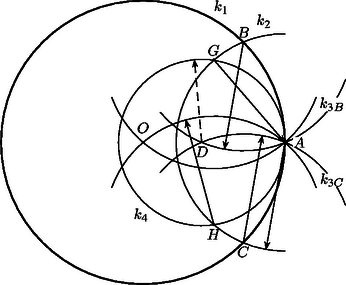
Legyen az adott $k_1$ körvonal megszerkesztendő középpontja $O$, a körvonal egy tetszőleges pontja pedig $A$. Rajzoljunk az $A$ mint középpont körül egy olyan $k_2$ kört, amelynek a sugara az adott körénél kisebb, annak felénél viszont nagyobb; messe ez a kör a $k_1$-et $B$-ben és $C$-ben. ($k_2$ megtalálása a szerkesztés egyetlen ,,véletlenszerű'' lépése; többszöri kísérletezéssel, illetve becsléssel oldhatjuk meg, pl. azt, hogy $k_2$ kisebb sugarú-e, mint $k_1$, úgy ellenőrizhetjük, hogy rámérhető-e ‐ ,,maradékkal'' ‐ hatszor a $k_1$-re.) Húzzuk meg ezután a $B$ és $C$ középpontú, egyaránt $AB$ sugarú $k_{3B}$ és $k_{3C}$ köröket. A $k_1$-en belül $k_{3B}$ és $k_{3C}$ metszéspontját $D$-vel jelöljük. Szerkesszük meg most a $D$ középpontú, $DA$ sugarú $k_4$ kört; $k_4$ és $k_2$ metszéspontjait jelölje $G$ és $H$.
Megmutatjuk, hogy a $G$ és a $H$ középpontú, $GA=HA\left(=AB\right)$ sugarú körök $A$-tól különböző metszéspontja éppen a keresett $O$ középpont. Jelöljük $k_1$ sugarát $R$-rel, $k_2$ sugarát $r$-rel, a $DCA$ szöget pedig $\alpha$-val. A $DCA$ egyenlő szárú derékszögű háromszögből $CDA\sphericalangle =CAD\sphericalangle ={90}^{\circ }-\frac{\alpha }{2}$, így $DA=2r\text{sin}\frac{\alpha }{2}$. Az $ABC$ háromszög köré írt kör $k_1$, és az $AB=r$ oldallal szemközti szög $\frac{\alpha }{2}$, ezért $R=\frac{r}{2\text{sin}\frac{\alpha }{2}}$. Mivel a $k_{3B}$ és $k_{2C}$ körök egymás tükörképei az $OA$ egyenesre vonatkozóan, azért $O$, $D$ és $A$ egy egyenesen fekszik; így $GAD\sphericalangle =OAG\sphericalangle$. Továbbá