Kezdőlap


Feladat:	Gy.3019	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bérczi Gergely , Bujdosó Attila
Füzet:	1996/március, 161 - 162. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Körülírt kör, Gyakorlat
Hivatkozás(ok):	Feladatok: 1995/november: Gy.3019

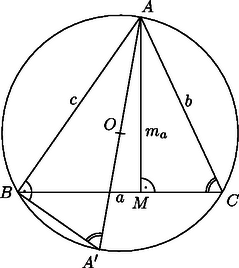
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismert, hogy ha egy háromszög oldalai $a$ , $b$ és $c$ , területe $T$ , a köré írható körének sugara pedig $R$ , akkor $T = \frac{a b c}{4 R}$ . (Ennek az állításnak a részletes bizonyítása megtalálható pl. Hajós György: Bevezetés a geometriába című könyvének 150. oldalán, de az 1. ábra segítségével az olvasó is könnyen elvégezheti a bizonyítást. Az ábrán $O$ a köré írható kör középpontja, $M$ pedig az $A$ csúcsból induló magasság talppontja. Az $A A' B$ és az $A C M$ háromszögek hasonlóak, ezért $\frac{c}{2 R} = \frac{m_{a}}{b}$ , amiből az állítás már következik.)
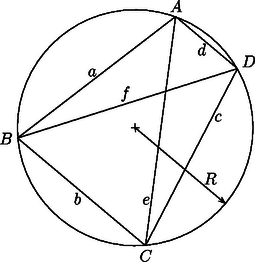
Legyen az $A B C D$ húrnégyszögben $A B = a$ , $B C = b$ , $C D = c$ , $D A = d$ , $A C = e$ és $B D = f$ (2. ábra). Az $A B C$ , $A D C$ , $A B D$ és $B C A$ háromszögek köré írható köreinek sugarai egyenlők, hiszen mindegyik kör éppen a húrnégyszög köré írható kör; ezért

\begin{matrix} T_{A B C} = \frac{a b e}{4 R} és T_{A D C} = \frac{c d e}{4 R} . \end{matrix}

(

R

a húrnégyszög köré írható kör sugara.) Így kapjuk, hogy

\begin{matrix} T_{A B C D} = T_{A B C} + T_{A D C} = \frac{a b e}{4 R} + \frac{c d e}{4 R} = \frac{e}{4 R} (a b + c d) . \end{matrix}

Másrészt a húrnégyszöget másik átlójával két háromszögre bontva

\begin{matrix} T_{A B C D} = T_{A B D} + T_{C B D} = \frac{a d f}{4 R} + \frac{b c f}{4 R} = \frac{f}{4 R} (a d + b c) . \end{matrix}

A húrnégyszög területére felírt kétféle egyenlőségből

\begin{matrix} \frac{e}{4 R} (a b + c d) = \frac{f}{4 R} (a d + b c) . \end{matrix}

Ezt az egyenlőséget

4 R

-rel szorozva éppen a bizonyítandó állítást kapjuk.

Bérczi Gergely (Szeged, Ságvári E. Gyak. Gimn., II. o.t.)