| Feladat: | Gy.3016 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Czirok Levente , Pál János , Szabó Jácint , Terpai Tamás | ||
| Füzet: | 1996/május, 279. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Indirekt bizonyítási mód, Rekurzív sorozatok, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1995/november: Gy.3016 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Tegyük föl, hogy van a számok között pozitív, legyen ezek közül (az egyik) legnagyobb az . Nyilván , hiszen . Az feltétel átrendezéséből , ami azt jelenti, hogy és közül legalább az egyik nem kisebb -nál. Mivel a számok legnagyobbika, ez csak úgy lehetséges, ha . Ezt ismételgetve adódik, ami ellentmond az feltevésnek. Ezzel az állítást igazoltuk. Megjegyzés. Terpai Tamás (Fazekas M. Főv. Gyak. Gimn., 8. o.t.) megoldásában rámutat, hogy a feladatban szereplő feltételek azt jelentik, hogy a , , , pontok összekötésével egy konvex függvénygörbét kapunk (lásd az ábrát), és ennek maximuma az értelmezési tartomány végpontja(i)ban van, hacsak nem konstans. Mindkét esetben tehát . 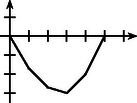 |