Kezdőlap


Feladat:	Gy.3005	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Bérczi Gergely , Méder Áron
Füzet:	1996/február, 85 - 86. oldal		PDF \| MathML
Témakör(ök):	Egyenes körhengerek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1995/szeptember: Gy.3005

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A henger alapkörének sugara $R = 50$ cm, magassága $M = 100$ cm, felszíne tehát

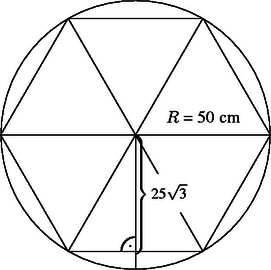
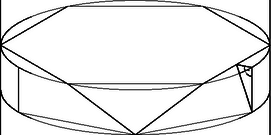
\begin{matrix} A_{h} = 2 π R (R + M) = 15 000 π {cm}^{2} < 48 000 {cm}^{2} . \end{matrix}

A beírt testet két szabályos hatszög és

100 \cdot 12 = 1200

egybevágó háromszög határolja. A háromszögek egyik oldala megegyezik az

R

sugarú körbe írt szabályos hatszög oldalával, vagyis 50 cm. Az ehhez az oldalhoz tartozó magasság egy olyan derékszögű háromszög átfogója, amelynek egyik befogója 1 cm (a hengert metsző síkok közül két szomszédos távolsága), a másik pedig

50 - 25 \sqrt[]{3}

cm (az

R

sugarú kör sugarának és a körbe írt szabályos hatszöget alkotó

R

oldalú szabályos háromszögek magasságának különbsége), tehát a magasság

m = \sqrt[]{{(50 - 25 \sqrt[]{3})}^{2} + 1} > 6

cm (2. ábra). Vagyis egy háromszög területe nagyobb, mint

\frac{50 \cdot 6}{2} = 150 {cm}^{2}

. Ezért a beírt test felszíne

\begin{matrix} A_{b} > 1200 \cdot 150 {cm}^{2} = 180 000 {cm}^{2} . \end{matrix}

Vagyis

A_{b} > A_{h}

, amit bizonyítani akartunk.

Méder Áron (Budapest, Táncsics M. Gimn., II. o.t.)

Megjegyzések. 1. Pontosabb számolással belátható, hogy a beírt test felszíne a henger felszínének több mint négy és félszerese. Az állítás akkor is igaz, ha a hengert nem 100, hanem csak 9 síkkal szeleteljük.
2. Ha egy henger magassága alapköre sugarának

α

-szorosa, a hengert

n

síkkal szeleteljük, és minden metszetkörbe szabályos

m

-szöget írva készítjük el a beírt testet, akkor annak felszíne

\begin{matrix} {[π (1 + α) - m sin \frac{2 π}{m}]}^{2} - 4 α^{2} sin^{2} \frac{π}{m} < n^{2} \cdot 4 sin^{2} \frac{π}{m} {(1 - cos \frac{π}{m})}^{2} \end{matrix}

teljesülése esetén lesz nagyobb a henger felszínénél.

Bérczi Gergely (Szeged, Ságvári E. Gyak. Gimn., II. o.t.)