Kezdőlap


Feladat:	1957. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1957/november, 95 - 96. oldal		PDF \| MathML
Témakör(ök):	Kör (és részhalmaza), mint mértani hely, Pitagorasz-tétel alkalmazásai, Arany Dániel
Hivatkozás(ok):	Feladatok: 1957/szeptember: 1957. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás: Megmutatjuk, hogy a feltételnek megfelelő háromszögek $C$ -ből induló súlyvonalai egyenlők. Legyen az $A B$ oldal hossza $c$ , és a $C$ pont $A B$ -n levő merőleges vetületének távolsága $A B$ felezőpontjától $x$ (4. ábr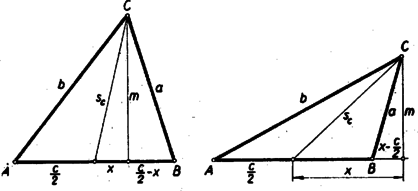a).

4. ábra

Ekkor Pythagoras tétele szerint

\begin{matrix} a^{2} = {(\frac{c}{2} - x)}^{2} + m^{2} = {(\frac{c}{2})}^{2} - c x + x^{2} + m^{2}, \\ b^{2} = {(\frac{c}{2} + x)}^{2} + m^{2} = {(\frac{c}{2})}^{2} + c x + x^{2} + m^{2}, \end{matrix}

és

\begin{matrix} m^{2} + x^{2} = s_{c}^{2} . \end{matrix}

Így

\begin{matrix} d^{2} = a^{2} + b^{2} = 2 {(\frac{c}{2})}^{2} + 2 (x^{2} + m^{2}) = 2 {(\frac{c}{2})}^{2} + 2 s_{c}^{2}, \end{matrix}

vagyis

\begin{matrix} s_{c}^{2} = \frac{d^{2}}{2} - {(\frac{c}{2})}^{2} . \end{matrix}

Ennek az értéknek pozitívnak kell lennie, különben nem lehetséges olyan háromszög, amely kielégíti a feladat feltételeit. Mivel itt

d

és

c

adott, azért

s_{c}

hossza független a

C

pont helyzetétől. Az összes megfelelő pontok tehát rajta vannak az

A B

szakasz felezőpontja körül

\begin{matrix} r = \sqrt[]{\frac{d^{2}}{2} - {(\frac{c}{2})}^{2}} \end{matrix}

sugárral rajzolt körön.
Legyen fordítva

C'

egy tetszés szerinti pont ezen a körön, távolsága

A

-tól, illetőleg

B

-től

b'

, ill.

a'

. Ekkor az

A B C'

háromszög

C'

-ből kiinduló súlyvonala

r

, s így a fenti képlet szerint

\begin{matrix} \frac{d^{2}}{2} - {(\frac{c}{2})}^{2} = r^{2} = \frac{{a'}^{2} + {b'}^{2}}{2} - {(\frac{c}{2})}^{2} \end{matrix}

amiből következik, hogy

\begin{matrix} {a'}^{2} + {b'}^{2} = d^{2}, \end{matrix}

tehát a

C'

pont megfelel a mértani hely feltételeinek.
A keresett mértani hely tehát az

A B

szakasz felezőpontja körül

r

sugárral rajzolt kör.