Kezdőlap


Feladat:	1978. évi Nemzetközi Matematika Diákolimpia 12. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1978/október, 49 - 50. oldal		PDF \| MathML
Témakör(ök):	Helyvektorok, Vektorok lineáris kombinációi, Vektorok skaláris szorzata, Téglalapok, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1978/szeptember: 1978. évi Nemzetközi Matematika Diákolimpia 12. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először egy könnyen igazolható segédtételt mondunk ki: minden $A B C D$ téglalapra és minden (nem feltétlenül a téglalap síkjában lévő) $O$ pontra $O A^{2} + O C^{2} = O B^{2} + O D^{2}$ . Legyen ugyanis $\vec{A B} = a, \vec{B C} = b, \vec{O A} = x$ (a1. ábra), ekkor $a b = 0$ , hiszen $a$ és $b$ merőlegesek. A bizonyítandó állítás pedig az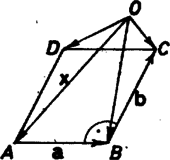

\begin{matrix} x^{2} + {(x + a + b)}^{2} = {(x + a)}^{2} + {(x + b)}^{2} \end{matrix}

azonosság átírása.

1. ábra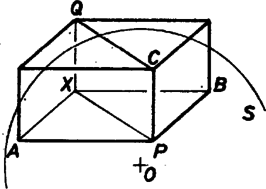

2. ábra

Térjünk rá a feladatra. Legyen az adott

S

gömb középpontja

O

, sugara

r

, az

A P B X

téglalap negyedik csúcsa

X

(2. ábra). A segédtételt az

A P B X

, valamint

P X Q C

téglalapokra alkalmazva kapjuk, hogy

\begin{ma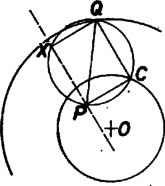trix} O P^{2} + O X^{2} = O A^{2} + O B^{2}, {O P}^{2} + O Q^{2} = O X^{2} + O C^{2}, \end{matrix}

ahonnan

\begin{matrix} O Q^{2} = O A^{2} + O B^{2} + O C^{2} - 2 O P^{2} = 3 r^{2} - 2 O P^{2} = állandó, \end{matrix}

azaz a

Q

pont rajta van az

O

középpontú,

r_{1} = \sqrt[]{3 r^{2} - 2 O P^{2}} > r

sugarú

S_{1}

gömbön.

3. ábra

Megmutatjuk, hogy az

S_{1}

gömb minden

Q

pontja hozzátartozik a mértani helyhez. Tekintsük ugyanis az

S

gömb és a

P Q

átmérőjű gömb metszésvonalát. Ennek az

O P Q

síkba eső egyik pontja legyen

C

és

Q C P

-t téglalappá kiegészítő negyedik pont

X

(3. ábra). A segédtétel szerint

O X^{2} = O Q^{2} + O P^{2} - O C^{2} = 2 r^{2} - O P^{2} > r^{2}

, azaz az

X

pont kívül van az

S

gömbön. Így az

X P

átmérőjű gömbnek valamint az

S

gömbnek a

P

-ben

C P

-re emelt merőleges síkban van két közös pontja: az egyik legyen

B

, az

X B P

-t téglalappá kiegészítő negyedik csúcs

A

. Az

A P, B P

C P

szakaszok páronként merőlegesek, az általuk meghatározott tégla negyedik csúcsa

Q

, továbbá

B

és

C

S

gömbön van. Elegendő tehát megmutatnunk, hogy

A

S

-en van. Ez viszont az

\begin{matrix} O A^{2} = O X^{2} + O P^{2} - O B^{2} = (2 r^{2} - O P^{2}) + O P^{2} - O B^{2} = r^{2} \end{matrix}

összefüggésből következik.

Megjegyzés. Ha nem azt követeljük meg, hogy

A, B

és

C

egy gömb felszínén legyenek, hanem hogy rendre három egymással koncentrikus gömb felszínén, a mértani hely továbbra is egy gömb felülete. A feladat tetszőleges dimenziójú gömbökre, például síkra is általánosítható.