Kezdőlap


Feladat:	1970. évi Nemzetközi Matematika Diákolimpia 22. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1971/november, 125 - 126. oldal		PDF \| MathML
Témakör(ök):	Nevezetes azonosságok, Magasságpont, Vektorok skaláris szorzata, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1970/szeptember: 1970. évi Nemzetközi Matematika Diákolimpia 22. feladata

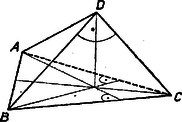
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1694. feladatban bebizonyítottuk,^{$^{*}$} hogy ha egy tetraéder egyik csúcsának a szemben levő lap síkján levő merőleges vetülete egybeesik annak a lapháromszögnek a magasságpontjával, akkor ez a tulajdonsága a tetraéder mindegyik csúcsának megvan.

Mostani feladatunk második feltevése szerint a

D

csúcsnak megvan a mondott tulajdonsága, ezért az

A

csúcsnak is; tehát

A

merőleges vetülete a

B C D

lap

S

síkján a

D

csúcs, hiszen az első föltevés szerint a

B C D

lap

D

-nél derékszögű háromszög, és így magasságpontja maga

D

. Ezek szerint

A D

merőleges

S

-re, és így ennek

D B

D C

egyeneseire is, tehát az

A D B

és az

A D C

háromszög is derékszögű, a tetraéder

D

-ből induló élei páronként merőlegesek egymásra.
Tetraéderünk származtatható egy téglatestből, elmetszve ezt a

D

csúcsában összefutó

3

él

A

B

C

végpontjaival meghatározott síkkal.
Alakítsuk az állítás jobb és bal oldalának

K

különbségét így:

\begin{matrix} K = 3 (A D^{2} + B D^{2}) + 3 (B D^{2} + C D^{2}) + 3 (A D^{2} + C D^{2}) - {(A B + B C + C A)}^{2} = \\ = 3 (A B^{2} + B C^{2} + C A^{2}) - (A B^{2} + B C^{2} + C A^{2}) - 2 (A B \cdot B C + B C \cdot C A + \\ + C A \cdot A B) = {(A B - B C)}^{2} + {(B C - C A)}^{2} + {(C A - A B)}^{2} . & (2) \end{matrix}

(Az első alak kéttagú kifejezéseit Pitagorasz tétele alapján helyettesítettük a megfelelő átfogó négyzetével, az utolsó alak tagjait pedig alkalmas csoportosítás alapján írtuk fel.)
(2) szerint

K

nem lehet negatív, tehát az állítás helyes. (1)-ben akkor és csak akkor érvényes az egyenlőségi jel, ha

K = 0

, azaz (2) mindhárom tagja külön is

0

, vagyis ha

A B = B C = C A

, a tetraéder

A B C

lapja szabályos háromszög, többi

3

lapja egybevágó egyenlő szárú derékszögű háromszög. A fent említett származtatás szerint kockából kiindulva kapunk ilyen tetraédert.

Engedi Antal (Makó, József A. Gimn. IV. o. t. )

^{$^{*}$}K. M. L. 41 (1970) 118. o.