Kezdőlap


Feladat:	1969. évi Nemzetközi Matematika Diákolimpia 12. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Cserepes L. , Dombi G. , Engedi A. , Fazekas Á. , Frankl P. , Füredi Z. , Gáspár Gy. , Hadik R. , Hermann T. , Horváth M. , Horváthy P. , Jakab F. , Kérchy L. , Láz József , Maróti Gy. , Martoni Viktor , Nagy Sándor , Pál J. , Pataki B. , Pressing L. , Prőhle T. , Pukler A. , Sashegyi L. , Simon Júlia , Taesó B. , Takács Helga , Turán Gy. , Vajnági A.
Füzet:	1970/március, 106 - 107. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletek, Trigonometriai azonosságok, Helyvektorok, Vektorok felbontása összetevőkre, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1969/szeptember: 1969. évi Nemzetközi Matematika Diákolimpia 12. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az addíció-tétel alapján átrendezve

\begin{matrix} f (x) = cos x (cos a_{1} + \frac{cos a_{2}}{2} + \frac{cos a_{3}}{2^{2}} + ... + \frac{cos a_{n}}{2^{n - 1}}) - \\ - sin x (sin a_{1} + \frac{sin a_{2}}{2} + \frac{sin a_{3}}{2^{2}} + ... + \frac{sin a_{n}}{2^{n - 1}}) = A cos x - B sin x, & (2) \end{matrix}

és itt az

A

és

B

kifejezéseknek legalább az egyike

0

-tól különböző, mert

f (x)

nem azonosan

0

. Valóban, az

x = - a_{1}

helyen (1) szerint

\begin{matrix} f (- a_{1}) = 1 + \frac{cos (a_{2} - a_{1})}{2} + \frac{cos (a_{3} - a_{1})}{2^{2}} + ... + \frac{cos (a_{n} - a_{1})}{2^{n - 1}}, \end{matrix}

és itt minden egyes számlálóra fennáll

cos (a_{i} - a_{1}) ≧ - 1 (i = 2,3, ..., n)

, ezért

\begin{matrix} f (- a_{1}) ≧ 1 - \frac{1}{2} (1 + \frac{1}{2} + ... + \frac{1}{2^{n - 2}}) = \frac{1}{2^{n - 1}} > 0. \end{matrix}

Ha mármost pl.

B \neq 0

, akkor

f (x)

zérus helyeire (2)-ből

\begin{matrix} tg x = \frac{A}{B}, \end{matrix}

és ha ennek

x_{1}

eleget tesz, akkor a

tg x

függvény periodikus volta alapján, és mert egy perióduson belül minden valós értéket egyszer vesz fel, minden más gyöke

\begin{matrix} x_{2} = x_{1} + m π \end{matrix}

alakú, hol

m

egész szám. Ebből adódik az állítás.
Ha pedig éppen

B = 0

, akkor

A \neq 0

, és így (2)-ből

\begin{matrix} cos x = 0, \end{matrix}

ennek zérus helyei

(4 k + 1) π / 2

és

(4 k + 3) π / 2

(ahol

k

egész), és könnyű belátni, hogy bármely kettőjüknek különbsége egész többszöröse

π

-nek.

Martani Viktor (Veszprém, Lovassy L. Gimn., III. o. t.)

II. megoldás. Válasszunk egy

O

kezdőpontot, és egy

O X

félegyenest alapiránynak, és rakjuk fel az

O A_{i}

vektort

(i = 1,2, ..., n)

, melynek abszolút értéke

1 / 2^{i - 1}

és irányszöge (ívmértékben)

a_{i}

. E vektorok

O X

irányú komponenseinek összege, ami ugyanaz, mint

O F

összegüknek

O X

irányú komponense, nyilvánvalóan az

f (0)

hosszúságú és

0

, ill.

π

irányszögű vektor aszerint, hogy

f (0) ≧ 0

, ill.

f (0) < 0

O F

nem

0

-vektor, mert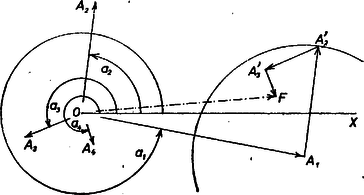

\begin{matrix} {\vec{O A}}_{1} + {\vec{O A}}_{2} = {\vec{O A}}_{1} = \vec{A_{1} A}'_{2} = \vec{O A}'_{2} \end{matrix}

abszolút értéke nem kisebb

1 / 2

-nél, hiszen

A'_{2}

A_{1}

középpontú,

1 / 2

sugarú kör kerületén van, és e körnek

O

-hoz legközelebbi pontja az

O A_{1}

szakasz felező-pontja. Ugyanígy kapjuk, tagról tagra képezve a részösszegeket, hogy

Q A_{n}

hozzáadása után

| O F | ≧ 1 / 2^{n}

Tetszőleges

x

-re (1) szerint úgy kapjuk az

f (x)

abszolút értékű és

0

vagy

π

irányszögű vektort, hogy mindegyik vektorunkat elfordítjuk

O

körül

x

ívmértékű szöggel, és így vesszük

O X

irányú komponensük összegét. Ezt egyszerűbben úgy is nyerhetjük, hogy

O F

-et fordítjuk el

x

-szel és ennek

O X

irányú komponense a mondott vektor.
Eszerint

f (x)

akkor és csak akkor

0

, ha

O F ⊥ O X

, az ezt eredményező

x

forgásszögek pedig

π

egész számú többszöröseiben különböznek egymástól. Ezzel az állítást bebizonyítottuk.

Láz József (Budapest, Eötvös J. Gimn., IV. o. t.)

Megjegyzés. Az I. megoldás

B = 0

esete azt jelenti, hogy

F

O X

egyenesen adódott.