Kezdőlap


Feladat:	Pontversenyen kívüli P.344	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Csere Kálmán , Pöltl János Tamás
Füzet:	1982/október, 71 - 72. oldal		PDF \| MathML
Témakör(ök):	Határozott integrál, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1981/január: Pontversenyen kívüli P.344

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Keressünk először a feltételeket kielégítő polinomokat, amelyek valamilyen $- 1 \leq x \leq 1$ mellett lehetőleg nagyok. Ha $x = 0$ , célszerűnek látszik a gyököket a $- 1$ , $+ 1$ pontokba tenni, Az $a (1 - x^{2})$ polinom tetszőleges $a > 0$ mellett nem negatív a [-1, 1] intervallumban, és ott az integrálja

\begin{matrix} \int_{- 1}^{1} a (1 - x^{2}) d x = a {[x - \frac{x^{3}}{3}]}_{- 1}^{1} = \frac{4 a}{3} . \end{matrix}

Ez akkor egyenlő 1-gyel, ha

a = \frac{3}{4}

. Ha

x = 1

, tegyük a függvény minimumát

(- 1)

-be, és legyen az értéke 0. Ez a

b {(1 + x)}^{2}

polinom, aminek az integrálja

\begin{matrix} \int_{- 1}^{1} b {(1 + x)}^{2} d x = b {[\frac{{(1 + x)}^{3}}{3}]}_{- 1}^{1} = \frac{8 b}{3} . \end{matrix}

Ez akkor egyenlő 1-gyel, ha

b = \frac{3}{8}

.
Az

a (x) = \frac{3}{4} (1 - x^{2})

és

b (x) = \frac{3}{8} {(1 + x)}^{2}

függvények képe

x = - 1

és

x = \frac{1}{3}

mellett metszi egymást, és

x \geq \frac{1}{3}

mellett

b (x) \geq \frac{2}{3}

- \frac{1}{3} \leq x \leq \frac{1}{3}

mellett

a (x) \geq \frac{2}{3}

. Mivel

x \leq - \frac{1}{3}

mellett a

c (x) = \frac{3}{8} {(1 - x)}^{2}

polinom értéke legalább

\frac{2}{3}

, és az

a (x)

b (x)

c (x)

polinomok mind szerepelnek azok között a polinomok között, amelyeknek

M (x)

a maximuma, tetszőleges

- 1 \leq x \leq 1

mellett

M (x)

értéke is legalább

\frac{2}{3}

. Nem is lehet máshol

\frac{2}{3}

M (x)

értéke, csak a

- \frac{1}{3}

+ \frac{1}{3}

helyeken, hiszen ha

x \neq \frac{1}{3}

, akkor max

[a (x), b (x), c (x)] > \frac{2}{3}

. Azt kell tehát még belátnunk, hogy például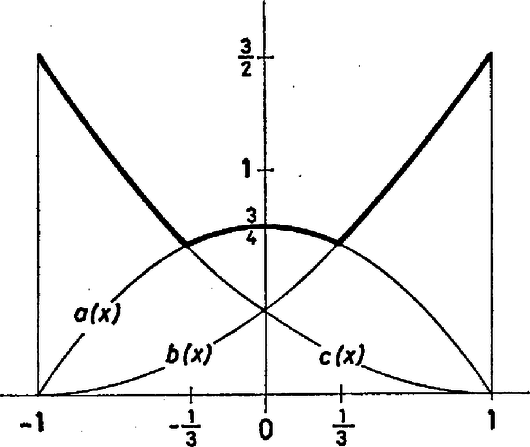

M (\frac{1}{3}) \leq \frac{2}{3}

Legyen

p (x) = a x^{2} + b x + c

tetszőleges másodfokú polinom, akkor

\begin{matrix} \int_{- 1}^{1} p (x) d x = \\ = {[\frac{a x^{3}}{3} + \frac{b x^{2}}{2} + c x]}_{- 1}^{1} = \frac{2 a}{3} + 2 c = \\ = \frac{1}{2} (a - b + c) + \frac{1}{2} (\frac{a}{3} + b + 3 c) = \\ = \frac{1}{2} p (- 1) + \frac{3}{2} p (\frac{1}{3}) . \end{matrix}

Ha tehát

p

integrálja

- 1

és

+ 1

között 1, és

p (- 1) \geq 0

, akkor

p (\frac{1}{3}) \leq \frac{2}{3}

, amint azt igazolni akartuk.