Kezdőlap


Feladat:	Pontversenyen kívüli P.309	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Beleznay Ferenc , Bölcsföldi László , Cseri István , Dénes László , Erdélyi Tamás , Fodor László , Gulács Ferenc , Hajnal Péter , Kiss 352 György , Komlósi Erzsébet , Németh Róbert , Simonyi Gábor , Szabó 457 László , Varga Lívia
Füzet:	1979/május, 213 - 214. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Euler-egyenes, Súlypont, Terület, felszín, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1978/november: Pontversenyen kívüli P.309

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismeretes, hogy a háromszöget bármelyik súlyvonalának egyenese két egyenlő területű részre osztja. Vajon van-e a súlyvonal egyeneseken kívül más olyan, a súlyponton áthaladó egyenes, amelyre ugyanez igaz?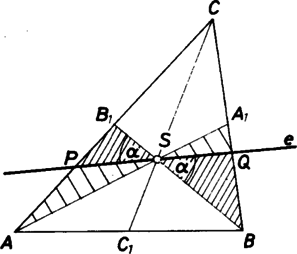
Indirekt módon bebizonyítjuk, hogy nincs.

Tegyük fel, hogy egy, az

A B C

háromszög

S

súlypontján átmenő

e

egyenes, amely egyik csúcson sem halad át, a háromszöget két egyenlő területű részre osztja. Ebből a feltevésből fogunk ellentmondásra jutni. Jelölje az

e

egyenesnek az

A C

, ill.

B C

oldalakkal alkotott metszéspontját

P

, ill.

Q

, ugyanezen oldalak felezőpontját

B_{1}

, ill.

A_{1}

.
A területfelezési tulajdonságból következik, hogy

P S B_{1} = Q S B

. (Valamely

X Y Z U ...

sokszög területét is

X Y Z U

-val jelöljük.) Ugyanis egyrészt

A B_{1} B = B B_{1} C

, másrészt

C P Q = Q P A B

. Ezekből az

\begin{matrix} A P S B + P B_{1} S = C B_{1} S Q + Q S B és \\ C B_{1} S Q + P B_{1} S = A P S B + Q S B \end{matrix}

egyenlőségeket kapjuk. Ezek összeadásával

P B_{1} S = Q S B

, amint azt állítottuk.
Ez utóbbiból a jól ismert területképlet felhasználásával az

\begin{matrix} \frac{S B_{1} \cdot P S \cdot sin α}{2} = \frac{S Q \cdot S B \cdot sin α}{2} \end{matrix}

összefüggéshez jutunk

(α = B_{1} S P ∢)

.
Ebből, mivel

B S = 2 B_{1} S

, következik, hogy

P S = 2 S Q

. De

A S = 2 A_{1} S

is igaz, s ezért az

A S P

és

A_{1} S Q

háromszögek hasonlók, hiszen két oldal arányában és a közbezárt szögben megegyeznek. Ebből a hasonlóságból

A P ∥ A_{1} Q

következik, ez pedig ellentmondás.
Az

e

Euler-egyenes átmegy a súlyponton, magasságponton és a körülírt kör középpontján. Az előbb bizonyítottak miatt

e

egybeesik valamelyik súlyvonal egyenesével, mondjuk

C S

-sel. Az

M

magasságpontra két eset lehetséges:
1.

M \equiv C

, akkor a háromszög derékszögű, s a körülírt kör középpontja egybeesik

C_{1}

-gyel.
2. Ha

M ≢ C

, akkor, mivel

C M ⊥ A B

és

C M

egyenese a súlyvonal egyenese,

A C = B C

, azaz a háromszög egyenlő szárú.
A mondottakból nyilvánvaló, hogy ezek és csak ezek a háromszögek rendelkeznek a kívánt tulajdonsággal.

Szabó 457 László (Csongrád, Batsányi J. Gimn., III. o. t.)