Feladat: Pontversenyen kívüli P.189 Korcsoport: 16-17 Nehézségi fok: -
Megoldó(k):  Bezdek A. ,  Csuka G. ,  Kelemen D. ,  Kiss E. ,  Lelkes A. ,  Páles Zs. ,  Surján P. 
Füzet: 1974/május, 217 - 218. oldal  PDF  |  MathML 
Témakör(ök): Mátrixjátékok, Logikai feladatok, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1973/november: Pontversenyen kívüli P.189

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Péter azt szeretné elérni, hogy legyen két egyező sor, vagy oszlop, vagy pedig legyen olyan sor, vagy oszlop, amelyikben mindegyik szám 0.
Ha Péter kezd, kövesse a következő stratégiát. Jelölje a négyzeteket A,B,...,I-vel az 1. ábra szerint, és alkosson párokat a B-C, E-F, H-I, D-G négyzetekből.

 

 

1. ábra
 

Először írjon A-ba tetszőleges számot, aztán akárhová ír Pál, annak a négyzetnek a párjába írja ugyanazt a számot, amit Pál. Ezzel eléri, hogy a BEH, CFI oszlopok egyezőek, tehát nyer.
Ha Pál kezd, feltehetjük, hogy először az A négyzetbe ír. Ha ugyanis nem ezt tenné, cseréljük fel az 1. sorral és az 1. oszloppal azt a sort, illetve azt az oszlopot, ahova Pál írt, és ezután kövessük a következő eljárást. Ha Pál 0-t írt A-ba, írjon Péter egy még üres sor és még üres oszlop közös négyzetébe 0-t. Erről az előbbiekhez hasonlóan feltehetjük, hagy E-be írta. Így Pál máris vesztésre áll, ugyanis Péter legközelebb ismét 0-t írhat vagy B-be vagy D-be ügy, hogy ennek a 0-nak a sorában is, oszlopában is két 0 és egy üres négyzet legyen, és e két nyerési lehetőség közül Péter csak az egyiket tudja megakadályozni (2. ábra).
 

 

2. ábra
 

Ha Pál az A-ba 1-es beírásával kezd, Péter ekkor is E-be írjon 0-t. Pál következő lehetőségei közül elég azokat tekintenünk, ha az ábra jobbra lejtő átlójától jobbra levő B, C, F négyzetbe ír valamit, vagy I-be, hiszen A=1 és E=0 után ez az átló még szimmetriatengely. Bármelyikbe ír, csak 1-est írhat, hiszen B-be vagy F-be írva 0-t, Péter azonnal nyer, ha pedig G-be vagy I-be ír 0-t, Péter az F-be írt 0-val ismét kettős nyerési lehetőséget szerezhet és a harmadik beírásával már nyer,
De Pál a második 1-es beírásával is csak késleltetheti Péter nyerését; ha B-be írja, akkor Péter F=0-val válaszol, a többi három esetben H=0-val. Pál mindenképpen az azonnali vesztés (3 db 0 egy vonalon) megakadályozására kényszerül D-be, illetve, B-be írt 1-essel. Válaszoljon Péter rendre az I-ben, G-ben, C-ben, D-ben 0-val, így Pál mindegyik esetben csak egy az előbbihez hasonló kényszerlépést tehet, végül Péter a második oszlopot valamelyik szomszédjával egyezővé téve nyer. (A 3. ábrán az indexek a beírás időbeli sorrendjét jelzik, Pál indexei páratlanok; a középső rész egybefoglalja Pál C-re és F-re írt 1-esének folytatását. ‐ Egyébként ha Pál az I-re írja második 1-esét, az ábra átlós szimmetriatengelyei alapján B, D, H és F egyenértéki mezők.)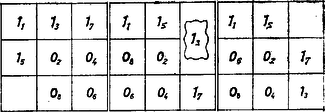
 

 

3. ábra
 

Ezzel beláttuk a feladat állításának helyességét.