| Feladat: | Pontversenyen kívüli P.140 | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Bara T. , Császár Gy. , Erdős P. , Stachó T. | ||
| Füzet: | 1975/január, 25 - 26. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Sokszög lefedések, Egyéb sokszögek geometriája, Pontversenyen kívüli probléma | ||
| Hivatkozás(ok): | Feladatok: 1972/április: Pontversenyen kívüli P.140 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Nevezzük a sokszög három csúcsát lefedő hármasnak, ha az általuk meghatározott kör lefedi a sokszöget. Egy fedő hármas mérete legyen az a legkisebb természetes szám, amelyhez megadható a sokszög szomszédos csúcsa úgy, hogy azok között a mondott három csúcs is szerepel. Azt fogjuk megmutatni, hogy a minimális méretű fedő hármas mérete , azaz a benne szereplő csúcsok szomszédosak. 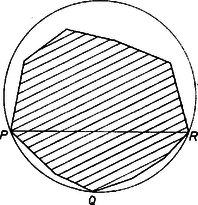 Nézzük meg, mekkora szög alatt látszik ezekből a szakasz, és válasszuk azt a csúcsot, amelyre ez a látószög maximális. Jelöljük ezt a csúcsot -sel, akkor , , fedő hármas, és mérete -nál kisebb. Ez utóbbi nyilvánvaló, az előbbi pedig következik abból, hogy e maximális látószög sem lehet nagyobb, mint az eredeti kör -et nem tartalmazó ívéhez tartozó kerületi szög. Emiatt a egyenes -et tartalmazó oldalán az eredeti kör teljes egészében az új körben van benne, -et nem tartalmazó oldalán pedig, választása miatt van minden csúcs benne az új körben. , tehát nem volt minimális, ellentmondásra jutottunk. Állításunkat ezzel bebizonyítottuk. |