Kezdőlap


Feladat:	Pontversenyen kívüli P.105	Korcsoport: -	Nehézségi fok: nehéz
Megoldó(k):	Horváth László , Szendrei Ágnes , Szendrei Mária , Tóth Gábor , Totik Vilmos , Turi Erzsébet , Zombory József
Füzet:	1973/május, 215 - 219. oldal		PDF \| MathML
Témakör(ök):	Ellipszis egyenlete, Parabola egyenlete, Terület, felszín, Helyvektorok, Ellipszis, mint kúpszelet, Parabola, mint kúpszelet, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1971/május: Pontversenyen kívüli P.105

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A parabola belsején a parabola vonalával kettévágott síknak azt a részét értjük, amelyikben a fókusz van és ehhez hozzáértjük magának a vonalnak a pontjait is. Így a beírandó ellipszisvonalnak lehet közös pontja az adott parabolákkal. Ha ezt kizárnánk, ‐ akkor mint könnyen belátható ‐ nem is lenne legnagyobb területű a beírt ellipszisek közt.
Koordinátákkal jellemezve a két parabola belsejének közös részét ‐ amit gyümölcsmagra emlékeztető alakja alapján $M$ -mel jelölünk ‐ azok az $(x, y)$ pontok alkotják, amelyekre ( $p$ -t természetesen pozitívnak véve) teljesül

\begin{matrix} x^{2} - p^{2} \leq 2 p y \leq p^{2} - x^{2} . \end{matrix}

(3)

Ez az

(x, y)

-nal egyidejűen teljesül a

(- x, y)

, a

(- x, - y)

és az

(x, - y)

pontra is, tehát

M

-et önmagába viszi át az

x

és

y

tengelyre való tükrözés és az origóra mint centrumra való tükrözés is.
2. Megmutatjuk, hogy

M

konvex idom, vagyis bármely két belső vagy kerületi pontját összekötő szakasz is benne van

M

-ben. Legyenek

P_{0} (x_{0}, y_{0})

és

P_{1} (x_{1}, y_{1})

a (3)-at teljesítő egymástól különböző pontok, ekkor, amíg

0 \leq λ \leq 1

, addig az

\begin{matrix} x_{λ} = (1 - λ) x_{0} + λ x_{1}, y_{λ} = (1 - λ) y_{0} + λ y_{1} \end{matrix}

koordinátájú

P_{λ}

pont végigfut a

P_{0} P_{1}

szakaszon és teljesíti (3)-at. Ugyanis egyrészt

\begin{matrix} 2 p y_{λ} = (1 - λ) \cdot 2 p y_{0} + λ \cdot 2 p y_{1} \leq (1 - λ) (p^{2} - x_{0}^{2}) + λ (p^{2} - x_{1}^{2}) = \\ = p^{2} - {(1 - λ) x_{0}^{2} + λ x_{1}^{2}} \leq p^{2} - {(1 - λ) x_{0} + λ x_{1}}^{2} = p^{2} - x_{λ}^{2}, \end{matrix}

hiszen

\begin{matrix} (1 - λ) x_{0}^{2} = {(1 - λ)}^{2} x_{0}^{2} + λ (1 - λ) x_{0}^{2}, \\ λ \cdot x_{1}^{2} = λ^{2} x_{1}^{2} + λ (1 - λ) x_{1}^{2} és \\ x_{0}^{2} + x_{1}^{2} \leq 2 x_{0} x_{1} . \end{matrix}

Másrészt lényegében ugyanígy bizonyítható,hogy

\begin{matrix} x_{λ}^{2} - p^{2} \leq 2 p y_{λ} . \end{matrix}

Megmutatjuk még az

M

-ből az I. síknegyedbe eső

M_{1}

résznek egy felhasználandó tulajdonságát is. Ennek pontjaira (3) jobb oldala szerint

\begin{matrix} x^{2} + y^{2} \leq p^{2} - 2 p y + y^{2} = {(p - y)}^{2}, \end{matrix}

azaz

r = \sqrt[]{x^{2} + y^{2}}

jelöléssel

\begin{matrix} r + y \leq p \end{matrix}

(3a)

És ha a pontot az

O

origó körül ráfordítjuk az

x

tengely pozitív felére,

r

változatlan marad,

y

lecsökken

0

-ra, tehát (3a) teljesül, a pont benne marad

M_{1}

-ben.
3. Az eddigiek alapján belátjuk, hogy ha egy

L

ellipszis benne van

M

-ben, akkor benne van az a vele egybevágó

L_{1}

ellipszis is, amelynek nagytengelye az

x

tengelyen van és kistengelye az

y

tengelyen. Erre támaszkodva elég lesz az

L_{1}

-gyel megegyező tengelyállású ellipszisek közül az

M

-be beírt legnagyobb területűt meghatároznunk.
Első lépésül azt látjuk be, hogy

L

-lel együtt az az origó középpontú

L_{0}

ellipszis is az

M

-ben van, amely

L

-ből a

\vec{C O}

eltolással áll elő, ahol

C

L

középpontja. Legyen

L

egy tetszőleges pontja

P

(a belsejében vagy a kerületén), ennek

C

-re való tükörképe

P'

, és

P'

-nek

O

-ra való tükörképe

P''

(1. ábr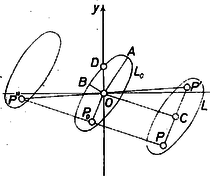a).

1. ábra

Mivel

L

centrálszimmetrikus, azért

P'

is az

L

-nek pontja és vele együtt

M

-nek is. Így pedig

P''

is az

M

-nek pontja, hiszen

M

is centrálszimmetrikus. A két tükrözés összetételeként

P''

előáll a

P

-ből transzlációval, melynek vektora

\begin{matrix} \vec{P P''} = \vec{P P'} + \vec{P' P''} = \vec{2 C P'} + \vec{2 P' O} = 2 \vec{C 0} . \end{matrix}

Ezért

M

konvex volta miatt a

P P''

szakasz

P_{0}

felezőpontja is benne van

M

-ben, másrészt

P_{0}

előáll a

P

-ből a

\vec{C O}

-ral való eltolással is. Ezt

P

helyén az

L

minden pontjára alkalmazva azt kaptuk, hogy a mondott

L_{0}

valóban benne van

M

-ben.
Föltehetjük, hogy

L_{0}

nagytengelye az első és harmadik síknegyedben van vagy ezek határán, hiszen ha nem így van, akkor ez az

x

tengelyre vett tükörképére áll fenn, és az is

M

-ben van. Jelöljük

L_{0}

nagytengelyének első negyedbeli végpontját

A

-val, kistengelye második negyedbeli végpontját

B

-vel, a rövidebbik

A B

ellipszisívnek az

y

tengelyen levő pontját

D

-vel és forgassuk

L_{0}

-t a negatív forgásirányban addig, míg

A

x

tengelyre ér. Eközben az

A O D

szögtartománybeli rész

M_{1}

ben marad, a

D O B

szögtartománybeli rész pedig belejut az

O D

sugarú körnek egy cikkébe, amely szintén

M_{1}

-ben van, hiszen

O B \leq O D \leq O A

. Tehát az

A O B

negyedellipszis elforgatottja

M_{1}

-ben lesz,

L_{0}

elforgatottja pedig ‐ a fent mondott

L_{1}

‐ az

M

-ben, ezt akartuk bizonyítani.
4. Eszerint ellipszisünk egyenlete

\begin{matrix} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1, | y | = \sqrt[]{b^{2} - \frac{b^{2} x^{2}}{a^{2}}}, a \geq b > 0 \end{matrix}

(4)

alakú, és benne az

a

b

féltengelyhosszakat úgy kell meghatároznunk, hogy egyrészt ne legyen

M

-en kívüli pontja, azaz (3) és (4) alapján

\begin{matrix} | x | \leq a \leq p és \sqrt[]{b^{2} - \frac{b^{2} x^{2}}{a^{2}}} \leq \frac{p}{2} - \frac{x^{2}}{2 p}, \end{matrix}

(5)

‐ speciálisan

x = 0

esetén

b \leq p / 2

‐, másrészt területe, ami közismerten

t = a b π

, maximális legyen, vagyis az

a b

szorzat legyen maximális. Ekvivalens átalakításokkal (5)-ből

\begin{matrix} {(\frac{p}{2} - \frac{x^{2}}{2 p})}^{2} + \frac{b^{2} x^{2}}{a^{2}} - b^{2} = {(\frac{p}{2} - \frac{x^{2}}{2 p} - \frac{p b^{2}}{a^{2}})}^{2} + b^{2} (\frac{p^{2}}{a^{2}} - \frac{p^{2} b^{2}}{a^{4}} - 1) \geq 0, \end{matrix}

(6)

és az első háromtagú így írható:

\begin{matrix} \frac{p}{2} (1 - \frac{2 b^{2}}{a^{2}}) - \frac{x^{2}}{2 p} . \end{matrix}

(7)

Egyelőre csak az olyan ellipsziseket tekintjük, amelyekben

2 b^{2} \leq a^{2}

, ezekben (7) eltűnik, ha

\begin{matrix} | x | = p \sqrt[]{1 - \frac{2 b^{2}}{a^{2}}}, (< p) \end{matrix}

(8)

így (6) teljesüléséhez szükséges, de elegendő is, hogy a második háromtagúban

\begin{matrix} \frac{p^{2}}{a^{2}} - \frac{p^{2} b^{2}}{a^{4}} - 1 \geq 0 \end{matrix}

legyen, azaz csak olyan

b

-k jönnek szóba, amelyekre (rögzített

a

mellett)

\begin{matrix} b \leq \frac{a}{p} \sqrt[]{p^{2} - a^{2}}, a b \leq \frac{a^{2}}{p} \sqrt[]{p^{2} - a^{2}} (és b \leq \frac{a}{\sqrt[]{2}}) . \end{matrix}

(9)

Így az

a

-tól függő

\begin{matrix} \frac{t}{π} = \frac{a^{2}}{p} \sqrt[]{p^{2} - a^{2}} \end{matrix}

függvény maximumát kell keresnünk, ami nyilván ugyanott van, mint a következő függvényé:

\begin{matrix} \frac{p^{2}}{4 π^{2}} \cdot t^{2} = \frac{a^{2}}{2} \cdot \frac{a^{2}}{2} (p^{2} - a^{2}) . \end{matrix}

Itt a három tényező összege

p^{2}

, állandó, tudjuk viszont, hogy állandó összegű pozitív számok szorzata akkor és csak akkor maximális, ha a tényezők egyenlők. Ebből, majd (9) alapján itt csak a következő ellipszisről lehet szó:

\begin{matrix} a = \sqrt[]{\frac{2}{3}} p (= 0, 816 p), b = \frac{\sqrt[]{2}}{3} p (= \frac{a}{\sqrt[]{3}} = 0, 471 p), & (10) \\ t = a b π = \frac{2 π}{3 \sqrt[]{3}} p^{2} (= 1, 209 p^{2}) . \end{matrix}

5. Hátra van még a

2 b^{2} > a^{2}, a < \sqrt[]{2} b

, tengelyarányú ellipszisek esete.
Ezekben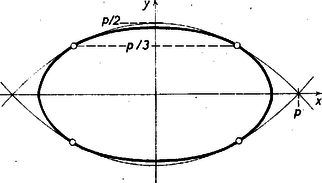

b \leq \frac{p}{2}

alapján

\begin{matrix} a \leq \frac{p}{\sqrt[]{2}} és a b π \leq \frac{π}{2 \sqrt[]{2}} p^{2} < \frac{2 π}{3 \sqrt[]{3}} p^{2}, \end{matrix}

azaz kisebb a fönt elért értéknél. Mindezek szerint a keresett ellipszis méreteit (10) adja, amely (8) szerint az

| x | = \frac{p}{\sqrt[]{3}}

abszcisszájú pontokban érinti

M

határát (2. ábra).

2. ábra

Egyenlete

x^{2} + 3 y^{2} = 2 p^{2} / 3

Megjegyzés. A 3. pont eredménye alapján vázolunk egy másik elindulást is. Nézzük meg, mit jelent az

a, b

tengelypárra, hogy (4) benne van

M

-ben. (3) jobb oldali egyenlőtlensége céljára (4) pontjaira

\begin{matrix} x^{2} + 2 p y = a^{2} (1 - \frac{y^{2}}{b^{2}}) + 2 p y = a^{2} + \frac{p^{2} b^{2}}{a^{2}} - {(\frac{p b}{a} - \frac{a y}{b})}^{2}, \end{matrix}

(11)

tehát (4) biztosan

M

belsejében van, ha

\begin{matrix} a^{2} + \frac{p^{2} b^{2}}{a^{2}} \leq p^{2} . \end{matrix}

(12)

Ha van (4)-nek olyan pontja, amelynek ordinátájára

\begin{matrix} \frac{p b}{a} - \frac{a y}{b} = 0, azaz y = \frac{b^{2}}{a^{2}} p, \end{matrix}

akkor (12) szükséges feltétele is annak, hogy (4) az

M

-beli legyen. Ilyen

y

akkor van, ha

\begin{matrix} \frac{b^{2}}{a^{2}} p \leq b, azaz p b \leq a^{2} . \end{matrix}

Ha viszont nincs ilyen

y

, azaz ha

p b > a^{2}

, akkor, mivel az ellipszis minden pontjára (11)-ben

\begin{matrix} \frac{p b}{a} - \frac{a y}{b} \geq \frac{p b}{a} - a > 0, \end{matrix}

ezt helyettesítve (11)-be

\begin{matrix} x^{2} + 2 p y \leq 2 p b, \end{matrix}

és ez nem nagyobb

p^{2}

-nél, ha

\begin{matrix} b \leq p / 2, \end{matrix}

(12)

ami triviálisan szükséges feltétele annak, hogy (4) az

M

-ben legyen.
Ha tehát valamely

b

-re teljesül (12), akkor (4) eleve

M

-beli minden olyan

a

mellett, melyre

p b > a^{2}

, vagyis amelynek a tengelyei ,,nem túl nagyok''. A

\sqrt[]{p b}

-nél nagyobb

a

értékekre pedig (12) a szükséges és elégséges feltétel. Ennek alkalmas továbbalakításából olvasható ki a fenti (10) eredmény.

Jutalmul 100‐100 Ft-os könyvutalványt kapott pontversenyen kívül: Bara Tamás, Bartolits István, Császár Gyula, Kiss Emil, Kollár János, Kópházi József, Lelkes András, Oláh Vera és Pallagi Dezső.