Kezdőlap


Feladat:	Pontversenyen kívüli P.59	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Balog János , Bendzsel Miklós , Boros Endre , Czédli Gábor , Duda Judit , Fábián Kristóf , Fejes Gábor , Ferró József , Filep János , Füredi Zoltán , Földvári Csongor , Győry György , Gödöllei Margit , Göndőcs Ferenc , Hermann Tamás , Horváth László , Horváth Mária , Horváth Miklós , István Mária , Iván László , Jász Péter , Juhász Júlia , Kertész András , Kirchner Imre , Kisvarga József , Lempert László , Lévai Gábor , Montvai György , Mózes László , Nagy Ferenc , Nagy István (Veszprém) , Páldi Vince , Pásztor Miklós , Pintér István , Poprádi Zsolt , Reviczky János , Simon Júlia , Sonkoly Pál , Tarsó Béla , Tóth Béla (Miskolc) , Török István , Vajnági András , Várady Tamás , Waszlavik László , Zágoni Miklós , Zámolyi Ferenc
Füzet:	1970/november, 147 - 150. oldal		PDF \| MathML
Témakör(ök):	Projektív geometria, Síkgeometriai szerkesztések, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1970/február: Pontversenyen kívüli P.59

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Köztudomású, hogy fényképen az egy egyenesen levő, egyenlő hosszú szakaszok képei általában különböző hosszúak, ezért a kívánt osztóvonalak képeit nem rajzolhatjuk meg (a pálya oldalvonalainak képén végrehajtott) szokásos szakaszfelezés, ill. harmadolás alapján.
A fényképet ‐ és eredetijét, a $φ$ felvételi filmet, ami sík ‐ centrális vetületnek tekinthetjük: egy (a felvevőgép látóterében, nyílásszögtartományában levő) $P$ pont vetülete (képe) a lencse $O$ középpontját vele összekötő egyenesnek, $P$ vetítősugarának $φ$ -vel való $P'$ metszéspontja, hiszen a $P$ -ből jövő és $O$ -n átmenő fénysugár irányváltozás nélkül halad a lencsén át a filmig. (A tárgyról jövő többi fénysugár az előbbivel a képpontban egyesül, csupán a vegyi hatást erősíti.) Tovább csak centrális vetületre gondolunk, $φ$ -t nem tekintjük határoltnak és csak azoknak a pontoknak tulajdonítunk vetületet, amelyek az $O$ -n átmenő, $φ$ -vel párhuzamos $φ_{0}$ sík által kettévágott térnek $φ$ -t nem tartalmazó felében vannak; már $φ_{0}$ -beli pontnak sincs vetülete.
Egy, az $O$ -n nem átmenő $e$ egyenes vetítősíkja az $O$ és $e$ által meghatározott sík, ennek $φ$ -vel való metszésvonala az $e$ -nek $e'$ képe, egyenes (pontosabban: csak akkor egyenes, ha $e ∥ φ$ és $e$ a mondott féltérben van; különben félegyenes képe félegyenes). Az $O$ -n átmenő egyenes képe pedig egyetlen pont.
Legyenek $e_{1}$ , $e_{2}$ egymással párhuzamos, az $O$ -n nem átmenő és a $φ$ -t metsző egyenesek. Vetületük, $e'_{1}$ , ill. $e'_{2}$ , metszi egymást egy pontban, hiszen az $O$ , $e_{1}$ és $O$ , $e_{2}$ vetítősíkok metszik egymást egy, az $O$ -n átmenő és amazokkal párhuzamos $e_{0}$ egyenesben, és ennek képén, ami egy $E_{0}$ pont, $e'_{1}$ is, $e'_{2}$ is átmegy. Ugyanígy minden az $e_{1}$ gyel párhuzamos egyenes vetülete átmegy $E_{0}$ -on.
Ezek alapján az $A B C D$ futballpálya (téglalap) $k$ középvonalának keresett $k'$ képe átmegy a kapuvonalak (alapvonalak) $A' B'$ , $C' D'$ képei meghosszabbításának $M'$ metszéspontján (1‐2. ábra).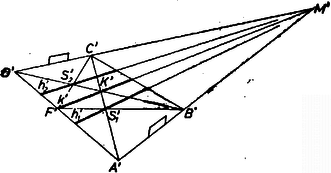

1. ábra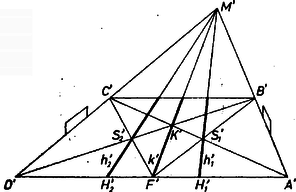

2. ábra

Másrészt

k

átmegy az

A C

B D

átlók metszéspontján, a pálya

K

középpontján, aminek képe az átlók képének

K'

metszéspontja; ennélfogva

k'

M' K'

egyenesnek a pálya

A' B' C' D'

képébe eső szakasza.
Ugyancsak

M'

-n megy át a

h_{1}

h_{2}

harmadolóvonalak keresett

h_{1}'

h_{2}'

képe is, egy-egy további pontjuk pedig az

A D B

, ill.

A D C

háromszög

S_{1}

, ill.

S_{2}

súlypontjának

S_{1}'

S_{2}'

képe, hiszen pl.

S_{1}

-nek

A B

-től való távolsága egyenlő az

A D

oldalvonal

1 / 3

részével. A két súlypont képét az

A K

B F

, ill.

D K

C F

súlyvonal-párok képeinek metszéspontja adja, ahol

F

A D

oldalvonal felezőpontja, aminek

F'

képét

k'

metszi ki

A' D'

-ből.
Szerkesztésünk csak olyan esetben nem hajtható végre, ha

A' B' ∥ C' D'

, azaz

M'

nem jön létre. Ez azt jelenti, hogy

A B

és

C D

vetítősíkjának metszésvonala nemcsak a pálya síkjával párhuzamos ‐ ami mindig fennáll ‐, hanem

φ

-vel is, ennélfogva e két sík (ti. a pálya és

φ

)

m

metszésvonalával is (oldalnézetben lásd a 3. ábrán).

3. ábra

Így pedig

k

h_{1}

és

h_{2}

képe is párhuzamos

m

-mel, vagyis

A' B'

-vel. Ezért

k'

K

-n át,

h_{1}'

h_{2}'

pedig a

k'

-ből

F'

útján nyert

S_{1}'

-n,

S_{2}'

-n át

A' B'

-vel párhuzamosan húzott egyenesszakasz (4. ábra).

4. ábra

‐ Lehetséges az is, hogy

m

sem jön létre,

φ ∥ S

; ekkor a pálya képe téglalap, a szerkesztés valódi nagyságban (torzulások nélkül) elvégezhető.

Nagy Ferenc (Budapest, I. István Gimn., IV. o. t.)

II. megoldás. Feladatunkat a szakasz felosztás ismert szerkesztése képi megfelelőjének végrehajtásával oldjuk meg, a fentiek és az alábbi észrevétel felhasználásával.
Az I. megoldás 2. ábráján

A' D' ∥ B' C'

, a pálya képe trapéz. Ebből könynyen adódik,^{$^{*}$} hogy

A' F' = F' D'

, és hasonlóan kaphatjuk, hogy pl.

h'_{1}

-nek

A' D'

-n levő

H_{1}'

metszéspontja harmadolja

A' D'

-t. Másrészt ekkor a 3. ábrán végzett meggondoláshoz hasonlóan

A' D'

párhuzamos

φ

-nek és a pálya

S

síkjának

m

metszésvonalával. Ezek szerint az

m

-mel párhuzamos egyeneseken levő, egyenlő hosszú szakaszok képe egyenlő hosszú.
Eszerint, ha a pálya bármely fényképén pl.

A'

-n át párhuzamost húzunk

m

-mel, ennek az

A' B'

C' D'

egyenesek közé eső

A' T'

szakaszát megfelezzük és megharmadoljuk rendre az

U'

V'

W'

pontokkal (képen az 5. ábra, alaprajzban a 6. ábra), akkor

k

képe az

M' U'

egyenes (ill. ennek a pálya képébe eső szakasza),

h_{1}

-é és

h_{2}

-é pedig

M' V'

, ill.

M' W'

. Valóban, ekkor

T'

tekinthető egy az

S

-ben levő

T

pont képének, melyre

A T

párhuzamos

m

-mel, ugyanígy

U'

V'

W'

A T

szakasz felező-, ill. harmadolópontjai képének, ekkor pedig

M' U'

M' V'

M' W'

a rendre

U

-n,

V

-n,

W

-n át

A B

-vel párhuzamosan húzott, tehát

S

-ben fekvő egyenes képe, ezek az egyenesek átteszik az

A U : A T = 1 : 2

, az

A V : A T = T W : A T = 1 : 3

arányt az

A D

oldalvonalra képük pedig kijelöli az osztópontokat

A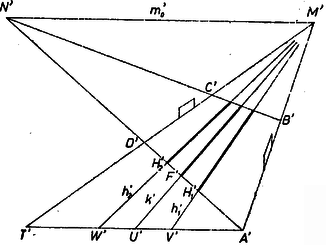' D'

-n.

5. ábra

6. ábra

A leírt szerkesztés céljára

m

irányát megadja az

O

-n átmenő és a pálya síkjával párhuzamos

S_{0}

síknak

φ

-vel való

m_{0}

metszésvonala (3. ábra). Ennek az

S_{0}

-nak egy pontja a fenti

M'

, mint az

O

-n át

A B

-vel párhuzamosan húzott, vagyis az

S_{0}

-ban fekvő egyenesnek a képe, egy másik pontja pedig ‐ ugyanezt a meggondolást az

A D

B C

párhuzamos egyenesekre megismételve ‐

A' D'

-nek és

B' C'

-nek

N'

metszéspontja.

Simon Júlia (Győr, Kazinczy F. Gimn., IV. o. t.)

Fejes Gábor (Miskolc, Földes F. Gimn., II. o. t.)

Megjegyzések. 1. Egyik megoldásban sem használtuk fel, hogy a futballpálya síkja vízszintes, sem azt, hogy a film síkja függőleges (különben e két tény egyike sincs biztosítva); számos dolgozat ezekre és ,,a perspektíva törvényeire'' épült, idézésük, megokolásuk nélkül.
2. A II. megoldás módján tetszés szerinti arányt rávihetünk egy, a fényképen levő egyenesszakaszra (hacsak a képen megvan egy rajta átmenő sík két párhuzamos egyenespárjának képe). Az I. megoldás szerint csak olyan

m : n

arányú osztást végezhetünk, melyre

m / n

racionális szám, és ismert egy, a szakaszt metsző párhuzamos egyenespár képe; ehhez is esetenként bonyolult meggondolás szükséges.
3. Érkezett olyan dolgozat is, amely azt használta fel, hogy egy-egy ,,szemben álló'' kapufa talppontját összekötő egyenes párhuzamos az oldalvonalakkal, és e 2 egyenes a pályát 3 téglalapra osztja fel. A fentiekben a kapukat csak a kapuvonalak és oldalvonalak megkülönböztetésére használtuk fel.

^{$^{*}$}Pl. az 1244. gyakorlat segédtételével, lásd K. M. L. 39 (1969) 62. o.